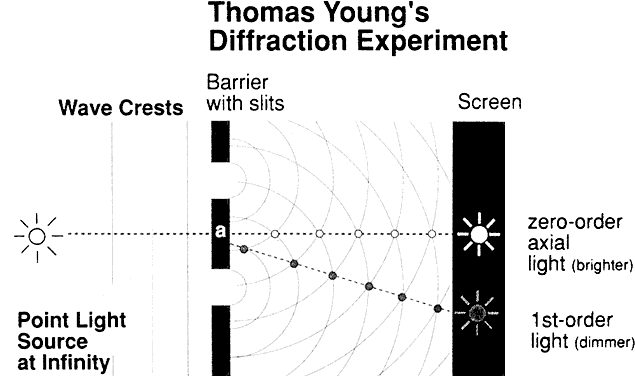
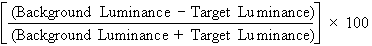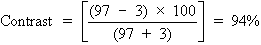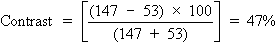DEFINITION Picture a shaft of light piercing a dusty room. The physicist sees each
dust particle as an agglomerate of many atoms and molecules. These, in
turn, are composed of negatively charged electrons and positively charged, heavy
nuclei. When a stream of photons is absorbed by a dust particle, the
electric field in the light beam can be pictured as exerting
an oscillating force on both the nuclei and the electrons. The heavy
nuclei remain unmoved, but the electrons are displaced from their normal
orbits and move rapidly back and forth in synchrony with the driving
electric field of the light beam. In so doing, light waves are radiated
in all directions. The observer sees the shaft of light because
his eye detects the sidewise-scattered light from each particle. If the
room were clean of all dust or scattering particles, the beam would
be invisible to the observer. The situation becomes a bit more complicated when the scattering particles
are spaced closer together than dust in a room. Certainly, each scattering
element radiates light waves in all directions, and the total
scattering is the sum of all the waves. But here is where a complication
arises. Waves may add constructively or destructively. At any one
observation outpost, the net amount of light reaching that point is determined
by the sum of the constructive and destructive interference of
all waves crossing that point. Let's stop for a moment for a definition. The quantity that describes
what point each wave is in its oscillation cycle is called the phase of the wave. The key concept in this definition is that the difference in phase between
waves depends, in part, on the spacings of the scattering particles
in comparison to the wavelength of light. If, for example, two scattering
particles are spaced by distances comparable to one half the wavelength
of light, the two scattered waves will be 180° out of phase
and the waves will then cancel each other, giving no electric field
at the observation point. If, however, two particles are spaced at distances
that are small in comparison to the light wavelength, the phases
will nearly be the same, and the scattered field will have an amplitude
twice as large as each wave individually. Therefore, the final summation
of all scattered waves will give a result that depends both on
the relative positions of each scattering particle in comparison to the
wavelength of light and on the direction of the scattered waves. For
example, light is completely transmitted through a transparent medium
such as water because the water molecules are tightly packed. This means
that all the waves scattered sideways from each of the molecules
travel a longer distance and are out of phase with each other and thus
interfere destructively with one another in all directions, except the
forward direction. In water, side-scatter is eliminated, but forward-directed
light waves reinforce each other because their straight-ahead
paths have similar lengths. Another factor important in scattering is the overall regular arrangement
of the scatterers. For example, the lens of the normal eye is made
up of protein and physiologic fluid. The lens proteins are tightly packed
in an orderly fashion, and there is very little change in the density
of the scattering particles from point to point in the lens. Thus, the
lens is transparent. If a clear lens homogenate is mixed with water, the
proteins are dispersed and the density of the proteins fluctuates
markedly, producing a random pattern. The result is a great deal of
scattering and a milky-appearing solution. In summary, the relationship between the size of the wavelength of light
involved, the spacing of the scatterers, the size of the scatterers, and
their arrangement determines the total scattering from a medium. This
interaction is analogous to running one's finger over a smoothly
polished surface. The surface feels smooth if the irregularities
are small in amplitude and are spaced by distances that are small in comparison
to the spacing between the pressure-sensitive receptors on the
fingertips. The sense of touch has a certain resolving power and cannot
respond to small-scale fluctuations. In the case of light and scattering, if
the scattering medium has periodic fluctuations in arrangements
of scattering components larger than the wavelength of light, then
these can be sensed by light waves and scattering can occur. If the
spacings of the scattering components of the media are shorter than one
half the light wavelength, little scattering can occur. It is time, now, to apply our theoretic understanding of light scattering. However, in
order to explain some natural phenomena we will need to
cover one more theoretic point. Lord Rayleigh showed that when light
strikes atmospheric particles (particles smaller than the wavelength
of light), the amount of light scattering is inversely proportional to
the fourth power of the wavelength. Since the blue end of the spectrum
is half the wavelength of the red end, the blue end is scattered by
a factor of 24 or 16 times the amount of the red end. This seems logical, since small
particles should interact more completely with smaller wavelengths. At high noon, the sun's rays pierce the atmosphere in a perpendicular
fashion (Fig. 4). Thus the shorter wavelengths of the sun's spectrum are more heavily
scattered by the atmospheric particles, which splash the color blue
all over the sky. This takes some of the blue away from the sun's
own appearance, and it looks yellowish. At sunset, the light strikes
the atmosphere at an angle and thus must travel a longer distance through
the atmosphere (see Fig. 4). The additional particles scatter not only blue but also a significant
amount of the longer wavelengths, and the sun's color goes from
yellow to orange to deep red. 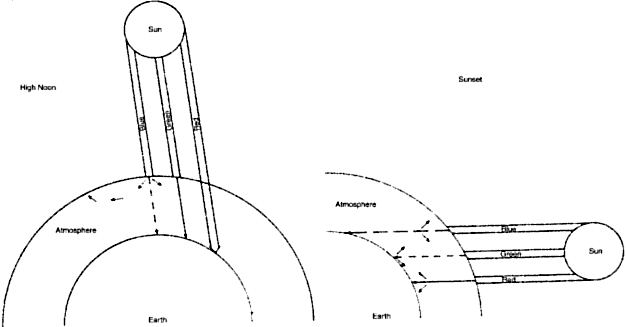 Fig. 4. At high noon, sunlight (a collection of all the colors) strikes the atmosphere
in a perpendicular fashion. Note: blue is scattered to a far greater
extent than green, which is scattered more than red. At sunset (left), the sun's rays travel a longer distance through the atmosphere. The
sun's rays encounter more atmospheric particles; thus, after
much of the blue has been scattered away, more of the green gets scattered. The
result is a redder sun at sunset. Fig. 4. At high noon, sunlight (a collection of all the colors) strikes the atmosphere
in a perpendicular fashion. Note: blue is scattered to a far greater
extent than green, which is scattered more than red. At sunset (left), the sun's rays travel a longer distance through the atmosphere. The
sun's rays encounter more atmospheric particles; thus, after
much of the blue has been scattered away, more of the green gets scattered. The
result is a redder sun at sunset.
|
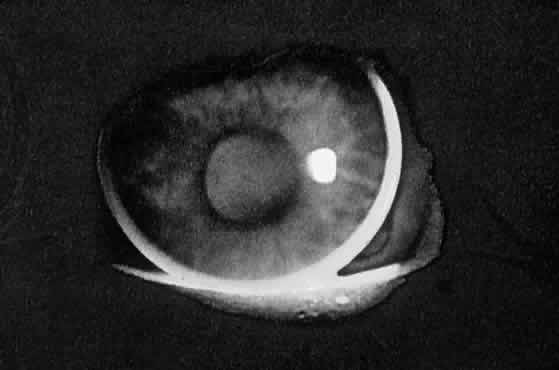
When you look at the lens of an elderly patient through the slit lamp, you
will notice that the reflection from the anterior capsule is blue-white, whereas
the reflection from the posterior capsule is a golden yellow. The
double passage of light through the lens has resulted in a
loss of blue light due to light scattering, producing the yellow reflection. The
more nuclear sclerosis present, the yellower is the reflection. Thus
we can think of the crystalline lens as a minus blue filter, because
of both its yellow pigment and its preferential scattering of
blue light. This concept of the lens as a minus blue filter was suggested by Dr. Aran
Safir2 and helps to explain why the optic nerve looks more yellow in the phakic
eye than in the aphakic eye. In fact, to the medical student, the blue-white
appearance of the optic nerve in the aphakic eye may be confused
with optic atrophy. In scleral tissue, we note that the collagen fibers are much larger than
those in the cornea. Both the collagen diameters and the spacing between
fibers are comparable to a light wavelength. Much scattering occurs
in the sclera, resulting in an opaque appearance. It might be helpful to return to nature for a moment and review what happens
when a sunbeam strikes a cloud. Clouds are made up of air and water
droplets, both of which are transparent; however, they differ in their
optical indices of refraction. Air has a refractive index of 1 and
water of 1.333. Thus, these two components, each clear by themselves, produce
substantial scattering when the droplets of water are large
enough to interact with the light waves and when the droplets are spaced
more than one half of a wavelength apart. Light scattering, then, is
what makes clouds look cloudy, scleras look white, and cataracts look
gray. We will now look at the clinical examples in more detail. NORMAL CORNEAL SCATTERING In the normal state,1 the cornea is essentially transparent. Experiments show that the corneal
stroma scatters approximately 10% of all light incident upon it.3 It is this small amount of scattering that allows us to see the corneal
structures under the slit lamp. But how can the cornea be so clear if it is made of structures as diverse
as epithelial cells, collagen fibers (refractive index, 1.47), and
a ground substance whose refractive index is close to that of water (1.333)? The
epithelial cell layer may be considered as homogeneous units
of a protein solution, with each cell so tightly packed against the
next that almost no extracellular water accumulates and there is virtually
no fluctuation in refractive index throughout the layers. In the
stroma, the collagen fibers are approximately 25 nm in diameter, and the
spacing between each pair of fibrils is 60 nm. These dimensions are
much smaller than a wavelength of yellow light (600 nm).4 Thus, the tiny dimensions and regular arrangement of these fibrils (Fig. 5) account for the minimal scattering.  Fig. 5. Top. Electron micrograph shows the arrangement of collagen fibers in normal
corneal stroma. Bottom. Electron micrograph of a corneal stroma with edema. Note the irregular
collection of fluid. (Miller D, Benedek G: Intraocular Light Scattering. Springfield, IL, Charles
C Thomas, 1973. Courtesy of T. Kuwabara, Howe Laboratory, Harvard
Medical School) Fig. 5. Top. Electron micrograph shows the arrangement of collagen fibers in normal
corneal stroma. Bottom. Electron micrograph of a corneal stroma with edema. Note the irregular
collection of fluid. (Miller D, Benedek G: Intraocular Light Scattering. Springfield, IL, Charles
C Thomas, 1973. Courtesy of T. Kuwabara, Howe Laboratory, Harvard
Medical School)
|
CORNEAL STROMAL EDEMA In cases of endothelial dystrophy, endothelial trauma, or endothelial incapacitation
due to inflammation (i.e., iritis), the pumping action of the endothelium diminishes and the stroma
takes on additional fluid and thickens. As interfibrillar fluid increases, the
collagen fibers are pushed farther and farther apart. As
the lakes of such fluid exceed one half of a wavelength of light in dimension, light
scattering increases and the cornea takes on a gray appearance (see Fig. 5).4 CORNEAL EPITHELIAL EDEMA In cases of advanced endothelial impairment or acute glaucoma, fluid collects
between the epithelial cells (Fig. 6). Fluctuations in the refractive index develop, and as the spaces between
the cells grow, the intensity of the scattering, or haze, grows. Potts
and Friedman5 have shown that in total corneal edema, the epithelial component accounts
for the greatest share of light scattering. 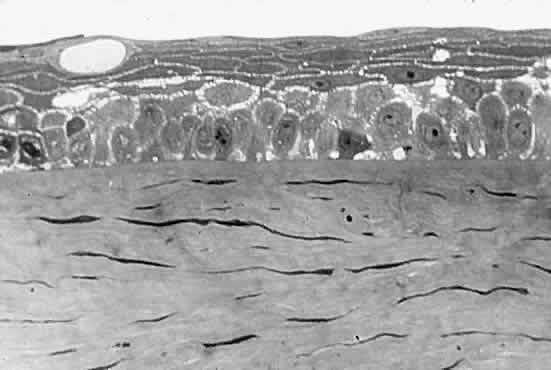 Fig. 6. Edematous epithelial layer of cornea as seen in a light micrograph. (Miller D, Benedek G: Intraocular Light Scattering. Springfield, IL, Charles
C Thomas, 1973. Courtesy of T. Kuwabara, Howe Laboratory, Harvard
Medical School) Fig. 6. Edematous epithelial layer of cornea as seen in a light micrograph. (Miller D, Benedek G: Intraocular Light Scattering. Springfield, IL, Charles
C Thomas, 1973. Courtesy of T. Kuwabara, Howe Laboratory, Harvard
Medical School)
|
CORNEAL SCARS When discontinuities in Bowman's membrane in ulceration, trauma, or
refractive surgery induces scar formation close to the pupillary center, visual
acuity decreases. Scars interfere with vision in two basic
ways: (1) they cause an irregularity of the corneal surface, producing
irregular astigmatism; (2) stromal scars contain either randomly arranged
collagen fibers, the diameters of which are five times the diameter
of normal corneal fibrils, or unusual material such as hyaluronic
acid, which pushes the collagen fibers far apart. This results in backscatter
of light, which yields a white appearance to the observer and
foggy vision to the patient. SCATTERING IN THE NORMAL LENS The normal lens is not as transparent as the normal cornea. This is partially
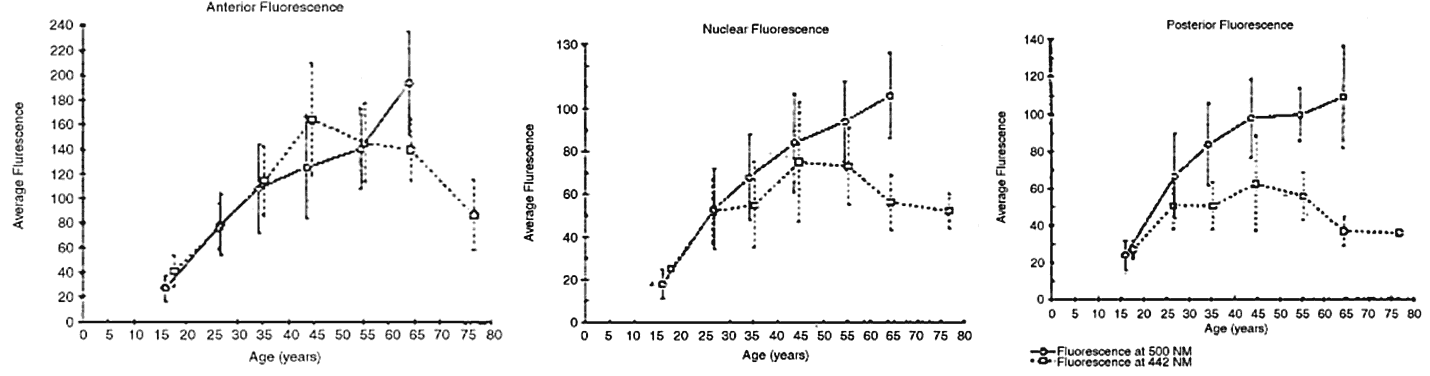
caused by the faint yellow pigment, which absorbs 10% to 40% of
all visible blue light. This hint of yellow is augmented by normal Rayleigh
scattering, present in the healthy lens. The normal clear lens, composed
of tightly packed high-protein-content lens fibers, scatters
a small amount of light. With aging, however, large protein aggregates
form within the lens fibers, reaching molecular weights of approximately 50 × 106 g/mol. CATARACT As a cataract develops, a normally uniform background of proteins is disturbed
by large lumps of protein aggregates. If these large lumps are
uncorrelated in position, and if the aggregates are large enough, significant
scattering will produce a turbid appearance. As the protein continues
to clump, fluid pools develop between lens fibers, and scattering
increases further. At some point in this progression, the clinician
decides to describe the patient's lens as cataractous. SCATTERING IN THE NORMAL VITREOUS The vitreous, a composite of a 1% hyaluronic acid solution, is interspersed
with collagen fibers of approximately 10 nm in diameter.6 These fibers are almost three times smaller than the normal corneal collagen
fibers. Since the scattering from each fiber is proportional to
the fourth power of the collagen diameter, we can expect the scattering
per fiber to be 80 times weaker for vitreous collagen than for corneal
collagen. Thus, the effect of the collagen in the vitreous is quite
small, and the vitreous will scatter only 0.1% of incident light. With
age, vitreous collagen fibrils coalesce, fluid pockets form, and localized
scattering develops to the point where the patient notices floating
specks and threads. RETINAL SCATTERING Because the ubiquitous Mu¯ller cells seem to squeeze tightly within
the spacings between the retinal cells, the tissue is homogeneous from
a refractive index standpoint and scatters about as much light as the
cornea. If, however, the blood supply to a retinal area is interrupted and infarction
takes place, the area fed by the occluded vessel becomes milky
gray. With infarction, edema fluid accumulates in the nerve fiber layer. Because
the refractive index of edema fluid differs from that of the
nerve fiber axons, the area loses transparency. GLARE The term “glare” is often used to describe the contrast-lowering
effect of stray light on a visual scene. The outfielder is said
to lose a fly ball into the sun because of glare. Extra light thrown onto
the retina tends to wash out the contrast of the event we are viewing. For
example, every student is aware of the importance of pulling
down all the shades and darkening the room if all the details of a slide
projected on a screen are to be appreciated. Because of the nature
of the light-detecting mechanism at the retina and in the brain, we cannot
see intensity differences efficiently in the presence of a high background
of light intensity. This sensitivity to glare is amplified as lens (or corneal) scattering
is increased. For example, the older surgeon cannot see the details within
a deep surgical wound in the presence of white surgical sponges.7 These sponges act as extraneous light sources, which are scattered by
the aging crystalline lens onto the macula of the surgeon's retina.8 Again, the patient with a poorly fitted contact lens who develops epithelial
corneal edema reports unusual glare from automobile headlights
at night. In cases of cataract or marked corneal edema, the patient has
difficulty reading in a bright environment, where all the elements of
normal light become sources of glare. This phenomenon is illustrated
in Figure 7. 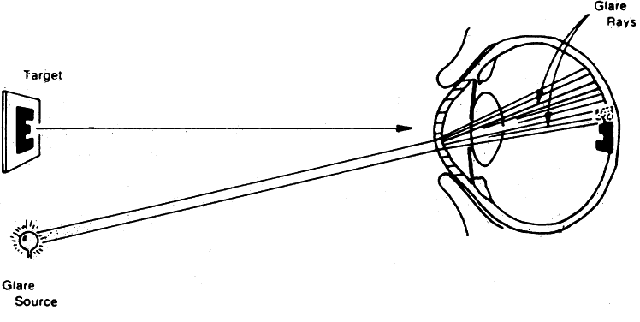 Fig. 7. Manner in which turbid cornea scatters off-axis light onto foveal image, thus
decreasing contrast of image. (Miller D, Wolf E, Jernigan ME et al: Laboratory evaluation of a clinical
glare tester. Arch Ophthalmol 87:329, 1972. Copyright © 1972, American
Medical Association) Fig. 7. Manner in which turbid cornea scatters off-axis light onto foveal image, thus
decreasing contrast of image. (Miller D, Wolf E, Jernigan ME et al: Laboratory evaluation of a clinical
glare tester. Arch Ophthalmol 87:329, 1972. Copyright © 1972, American
Medical Association)
|
Some time ago, we wondered what percentage of a lens must actually become
cataractous or, put another way, how much of the lens must remain clear
before scattering and consequent glare reach levels significant enough
to impair visual acuity. Although contrast started to drop slightly
when almost half the lens was “covered with cataract,” contrast
dropped suddenly when 80% of the lens became cataractous.9 Thus, light scattering, glare, and visual performance are all tightly bound
together. CLINICAL GLARE TESTING In 1926, the industrial scientist L.L. Holladay10 first described the relationship between glare and contrast sensitivity. Holladay
developed a mathematical relationship between the glare source (its
brightness and angular distance from the target) and contrast
sensitivity. In the 1960s, Ernst Wolf,8,11,12 a Boston visual physiologist, built a laboratory glare tester and showed
in a normal population that glare sensitivity increased with age. He
also showed that this increase in glare sensitivity was related to the
increased light scattering of the normal, aging lens. In the 1970s
and early 1980s, Miller, Wolf, Nadler, and others13,14 built and tested the first clinical glare tester (Miller-Nadler glare
tester; Fig. 8). With this device, they demonstrated a connection between cataract progress
and increased glare sensitivity.14 Figure 9 shows a plot of glare sensitivity versus visual acuity in 144 patients
with cataracts. What strikes one immediately is that the visual acuity
is randomly scattered throughout the plot, whereas glare sensitivity
increases in an orderly progression. Glare sensitivity also correlated
highly with the degree of posterior capsule opacification after extracapsular
cataract extraction and intraocular lens implantation.15  Fig. 8. The Miller-Nadler glare tester is an example of variable contrast target
using the Landolt ring surrounded by a glare source. (Nadler MP, Miller D, Nadler DJ: Glare and Contrast Sensitivity for Clinicians, p 27. New
York, Springer-Verlag, 1990) Fig. 8. The Miller-Nadler glare tester is an example of variable contrast target
using the Landolt ring surrounded by a glare source. (Nadler MP, Miller D, Nadler DJ: Glare and Contrast Sensitivity for Clinicians, p 27. New
York, Springer-Verlag, 1990)
|
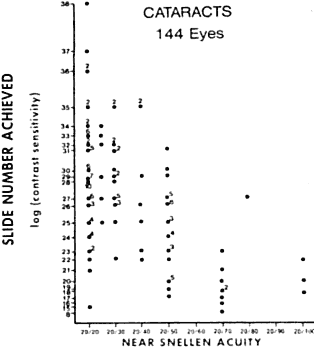 Fig. 9. Study of 144 patients with cataracts in which visual acuity versus glare
sensitivity was plotted. Note how many patients with increased glare
sensitivity had good visual acuity. (LeClaire J, Nadler MP, Weiss S, Miller D: A new glare tester for clinical
testing. Arch Ophthalmol 100:153, 1982) Fig. 9. Study of 144 patients with cataracts in which visual acuity versus glare
sensitivity was plotted. Note how many patients with increased glare
sensitivity had good visual acuity. (LeClaire J, Nadler MP, Weiss S, Miller D: A new glare tester for clinical
testing. Arch Ophthalmol 100:153, 1982)
|
GLARE TESTER CHARACTERISTICS Glare testers offer two types of targets: a standard Snellen visual acuity
chart and a variable contrast sensitivity target. The variable contrast
targets may be presented as (1) sinusoidal contrast gratings; (2) the
Snellen chart printed in different contrasts; or (3) the Landolt
ring presented in different contrasts. To determine whether a variable
contrast target or a standard visual acuity target would be more valuable
in cataract testing, we designed an experiment using scattering
filters of progressive severity (simulated cataracts).4,16 These laboratory experiments suggested that a variable contrast target
in the face of a glare source follows cataract progression more smoothly
than a conventional visual acuity target. QUANTIFICATION OF GLARE ON CONTRAST SENSITIVITY We have asserted that ocular lesions that scatter light degrade contrast
sensitivity by splashing extra noninformation containing light onto
the retinal image. This can be demonstrated by a simple calculation put
forth by Prager and colleagues.17 Suppose we wanted to measure the contrast of the standard projected Snellen
chart in both a darkened examining room and a lighted one. Contrast
is the difference between the luminance of the target and its background, and
can be expressed as a percentage, as follows: 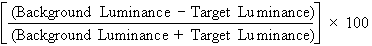
To calculate the contrast of the projected Snellen chart in a darkened
room, let us say the background illumination is 97 arbitrary light units, and
the target illumination (consisting of letters) is 3 light units. This
gives the following: 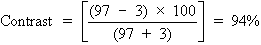
Let us now turn the room lights on, thus placing an additional 50 light
units onto both the background and letters of the projected Snellen chart. The
new contrast is given by the following: 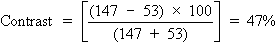
We see that this simple maneuver cuts the contrast in half. Just as the
Snellen chart drops its contrast when extra light falls upon it, the
retinal image loses contrast when a corneal lesion scatters extraneous
light onto the macula (see Fig. 7). There are a number of simple ways to decrease glare and improve contrast: - Using side shields on the temples of spectacles prevents glaring sidelong
rays from striking the eye (Fig. 10).
- Watching the television set with the room lights off prevents annoying
glare from ceiling or lamp light from striking the eye.
- Wearing polarized sunglasses will cancel out the reflected glare from shiny
surfaces (e.g., car hoods, lakes, glossy paper)
- Wearing a peaked cap or wide-brimmed hat prevents the overhead rays of
the sun from striking the eye.
- Replacing scratched or pitted automobile windshields reduces glare from
the sun and oncoming headlights.
 Fig. 10. Example from nature of a functional visor. Because the ground hornbill's
lids are prominent and its eyes recessed, a visor effect is created. (Colors in the Wind, p 25. Washington, DC, National Wildlife Federation, 1988) Fig. 10. Example from nature of a functional visor. Because the ground hornbill's
lids are prominent and its eyes recessed, a visor effect is created. (Colors in the Wind, p 25. Washington, DC, National Wildlife Federation, 1988)
|
Surgical Methods When these methods fail to help a patient who has glare disability, surgical
removal of the scattering lesion should be considered. Significant
corneal edema or permanent corneal scars can be treated by a corneal
transplant. A significant cataract should be extracted. Finally, an
opaque lens capsule after cataract surgery, which produces glare symptoms
or reduced contrast sensitivity, requires a capsulotomy. Because the
glare disability is proportional to the ratio of the area of capsule
opening over the area of capsule opacity, the size of the capsulotomy
must be considered. The size of the optimal capsulotomy equals the size
of the pupil (Fig. 11).18 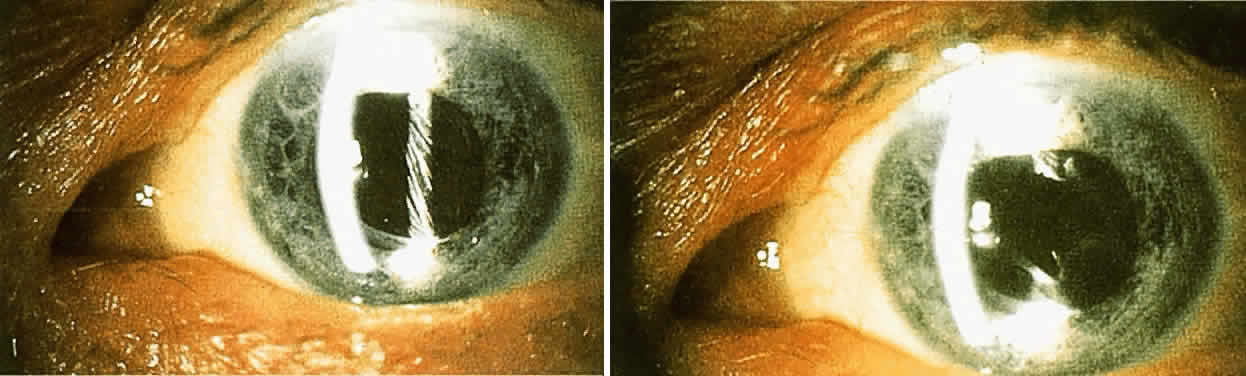 Fig. 11. Top. Opaque lens capsule (note diagonal lines in capsule). Bottom. Same capsule with laser-made opening. Fig. 11. Top. Opaque lens capsule (note diagonal lines in capsule). Bottom. Same capsule with laser-made opening.
|
|