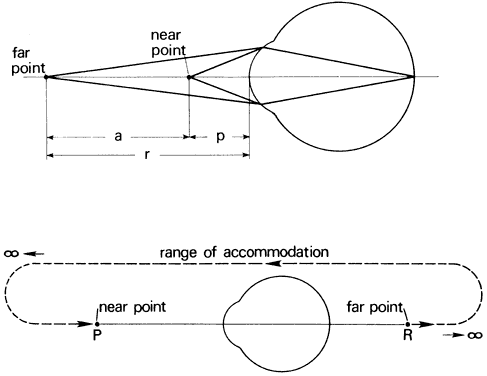
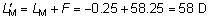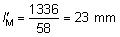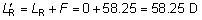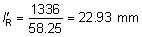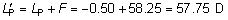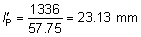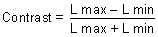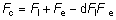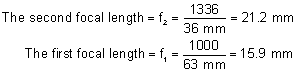Visual discrimination can be divided into three broad categories: light
discrimination, or the detection of light and color; spatial discrimination, or
the ability to distinguish forms and relationships in space; and
temporal discrimination, concerned with time-varying stimuli. Resolution
and acuity represent visual capacities within the category of
spatial discriminations. The total range of visual capacities are as
follows:- Light discrimination
- Brightness sensitivity or the ability to detect a very weak light
- Brightness discrimination or the ability to detect threshold changes or
differences in the luminance of light sources
- Brightness contrast having to do with luminance differences at levels well
above the threshold and their visual interactions
- Color discrimination or the ability to detect colors
- Spatial discrimination
- Types of visual acuity
- Minimum visible and perceptible acuity: the ability to detect the presence
of objects in the visual field without naming or resolving them
- Minimum separable acuity: the ability to resolve separate parts of a pattern
- Hyperacuity and vernier acuity: the ability to localize small displacements
of one part of an object with respect to the other parts
- Minimum legible acuity: the ability to recognize a pattern such as a letter
- Contrast sensitivity function of the eye
- Distance discrimination or ability to judge absolute or relative distances
of objects.
- Movement discrimination or the ability to detect relative or absolute angular
motion
- Temporal discrimination: the growth and decay of sensations caused by time-varying
stimuli, such as flickering lights
Light discrimination may not seem to be germane to the topic of the eye
as an optical system. However, it will be shown that visual acuity, resolution, and
spatial contrast sensitivity are related directly to discrimination
of brightness. The following discussion will deal with light
and spatial discriminations within the context of their influence
on acuity, resolution, and spatial contrast sensitivity. The density of rods and cones from the nasal to the temporal edge of the
retina (Fig. 38) is basic to an understanding of visual discrimination. Cones are concentrated
at the fovea and have a packing density that is about 18 times
greater than elsewhere in the retina. No rods occur at the fovea. They
reach maximum density at about 18 to 20 degrees from the fovea. Neither
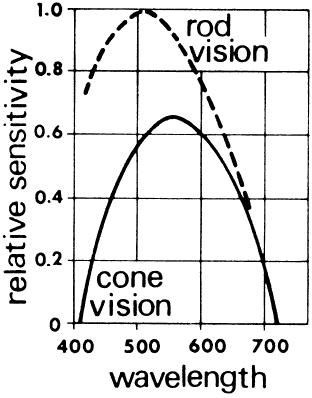
rods nor cones are found in the blind spot. Figure 39 illustrates the relative sensitivity to different wavelengths of light
of the rods and cones. Photopic vision for high-acuity discriminations
is mediated by the cones. The rods, sensitive to low light levels, are
used for scotopic vision. 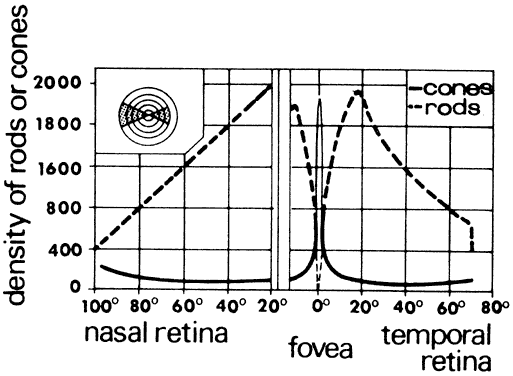 Fig. 38. Rod-cone population curve as measured across the shaded zone of the retina
in the inset figure. (Chapanis A: How we see. In: Human Factors in Undersea Warfare. Washington, DC: National
Research Council, 1949.) Fig. 38. Rod-cone population curve as measured across the shaded zone of the retina
in the inset figure. (Chapanis A: How we see. In: Human Factors in Undersea Warfare. Washington, DC: National
Research Council, 1949.)
|
LIGHT DISCRIMINATION Brightness Sensitivity Brightness sensitivity is the ability to detect a very weak light source
in a black background. Hecht and associates15 did the classic experiment to find the minimum energy necessary for vision. The
subject was dark-adapted for maximum sensitivity. They used
light of wavelength 510 nm corresponding to the peak spectral sensitivity
of the rods shown in Figure 39. A source subtending 10 minutes of arc, put 20' off-axis to correspond
with the area of greatest rod density was flashed on for 0.001 second. The detection threshold was found to correspond to approximately 50 to 150 photons
striking the cornea. Of these, about 50% are absorbed and
reflected by the ocular media, leaving 25 to 75 photons to strike the
retina. Only about 20% of these photons are absorbed by the rhodopsin, thus
only 5 to 15 photons are left to excite vision. Because they fall
on a 10-minute area of the retina that contains some 500 rods, the probability
of more than one photon falling on any rod is very low. Thus, the
light can be seen when each photon is absorbed by a different rod. When
one photon is absorbed, it is absorbed by one molecule of rhodopsin. This
single molecule initiates the chain of reactions, resulting
in nervous stimulation and the perception of light. Amazingly, a retinal
rod reaches the absolute limit of sensitivity set by quantum and
molecular theories. Brightness Discrimination Brightness discrimination is the ability to detect small differences in
brightness between two light sources, or luminance difference thresholds (LDTs). Given
two contiguous surfaces of the same color but slightly
different luminance, L and L + ΔL, the subject is to detect
the brighter surface; ΔL is equal to the LDT. The absolute threshold, described previously, is a special case of LDT
where L = 0 and shows the ability to detect light in a dark background. Brightness
discrimination, however, determines the ability to distinguish
the form and pattern of objects. Weber20 formulated a generalized expression applicable to brightness discrimination, stating
that for a difference to be detectable, it must be a nearly
constant fraction of the background luminance, or ΔL/L = constant. This
ratio is about 1% for brightness discrimination and was discovered
by Bouguer in 1760. Weber extended it to other senses. Actually
Weber's law breaks down at low and high levels of luminance. Brightness Contrast Expressed as a percentage, (ΔL/L) × 100 also is called brightness
contrast; ΔL is the difference in luminance between object
and background, and L is the brightness of the background. Brightness
contrast depends on the size of the object, the background brightness, the
wavelength, the region of the retina stimulated, and the shape
of the object. Figure 40 shows that smaller differences in brightness are required (lower contrast) as
illumination L increases. Larger objects require lower contrast
to be discriminated. 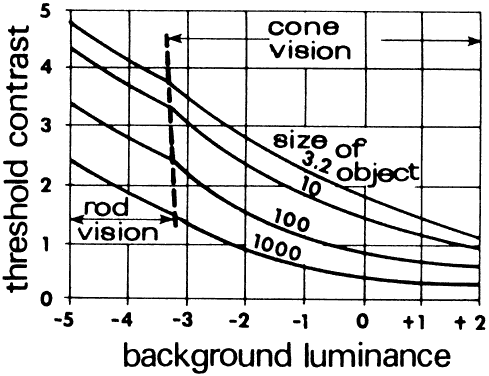 Fig. 40. Contrast discrimination curve. The least contrast required for an object
to be detected against its background decreases as the luminance (in
log units of millilamberts) increases. The eye can detect differences
in the brightness of objects better as the illumination increases. (Wulfeck JW et al: Vision in Military Aviation. WADC Technical Report
58–399. Wright Air Development Center, OH, Nov. 1959.) Fig. 40. Contrast discrimination curve. The least contrast required for an object
to be detected against its background decreases as the luminance (in
log units of millilamberts) increases. The eye can detect differences
in the brightness of objects better as the illumination increases. (Wulfeck JW et al: Vision in Military Aviation. WADC Technical Report
58–399. Wright Air Development Center, OH, Nov. 1959.)
|
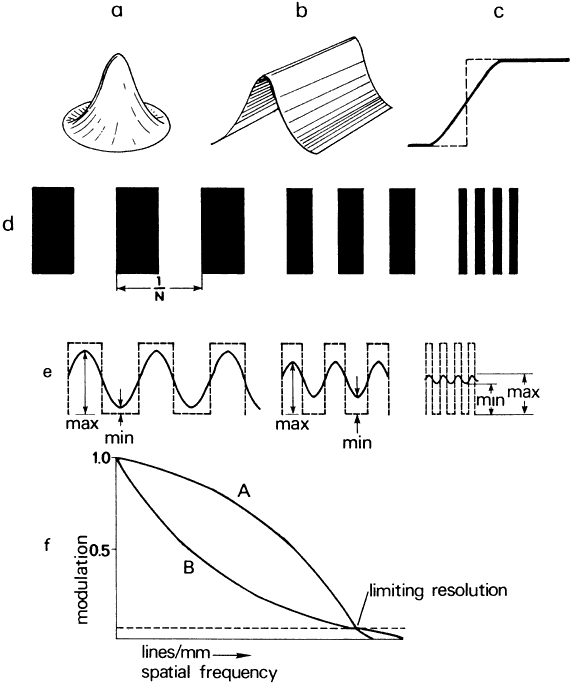
Spatial Contrast Sensitivity Visual acuity, measured with black Snellen letters on a white background, fails
to inform on the individual's ability to see targets of
low contrast that commonly make up the real world. A more complete assessment
of vision is provided by measuring the contrast sensitivity function (CSF). This
usually is done with spatial sine-wave patterns that
may be varied in contrast and spatial frequency (Fig. 41). Here, we define contrast as a ratio of luminances (L). 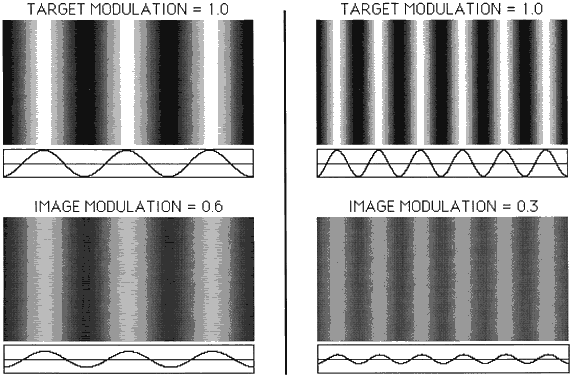 Fig. 41. Sine-wave gratings are shown at two spatial frequencies (left and right). The
top gratings are objects with high contrast (1.0), and contrast
is reduced to 0.6 and 0.3 at the bottom. Sinusoidal luminance profiles
are shown below each grating. Fig. 41. Sine-wave gratings are shown at two spatial frequencies (left and right). The
top gratings are objects with high contrast (1.0), and contrast
is reduced to 0.6 and 0.3 at the bottom. Sinusoidal luminance profiles
are shown below each grating.
|
Spatial frequency is the number of cycles per degree (cpd) in the sine-wave
pattern, where 30 cpd corresponds to 20/20 or 1 minute acuity. Contrast
sensitivity is the reciprocal of the threshold contrast or necessary
contrast for seeing the sine-wave pattern. A contrast sensitivity
curve, based on data by Corwin,16 is shown in Figure 42. The normal CSF curve shows that sensitivity falls at both high and low
spatial frequencies. Peak sensitivity lies at about 4 to 5 cpd. Thus, the
contrast thresholds are low at these spatial frequencies. 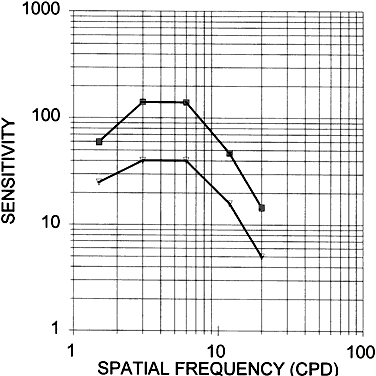 Fig. 42. Contrast sensitivity function (CSF). Mean CSF curve (top). Template for
rapid screening (below). (Corwin TR et al: Contrast sensitivity norms for the Mentor B-Vat II-SG
Video Acuity Tester. Optom Vis Sci 66:864, 1989) Fig. 42. Contrast sensitivity function (CSF). Mean CSF curve (top). Template for
rapid screening (below). (Corwin TR et al: Contrast sensitivity norms for the Mentor B-Vat II-SG
Video Acuity Tester. Optom Vis Sci 66:864, 1989)
|
Visual acuity is the end point of the CSF curve. Two individuals may have
the same Snellen acuity but very different sensitivities at intermediate
spatial frequencies. Contrast sensitivity decreases with age, cataracts, and
ocular and neural pathologies. Claims for using CSF diagnostically
have been controversial. However, CSF may be useful in monitoring
the efficacy of therapies or following vision changes after corneal
surgery. Several tests for clinical CSF measurements are available. The Mentor system
displays optotypes and sine-wave gratings on a monitor. Thresholds
are measured by a blocked up/down psychophysical procedure.16 The Arden17 and Vision Contrast Test System18 shown in Figure 43 comprise several printed sine-wave grating charts for distance and near
testing that provide a rapid assessment of CSF.  Fig. 43. Gratings that comprise the Vision Contrast Test System. Fig. 43. Gratings that comprise the Vision Contrast Test System.
|
Rapid results also are provided by the Pelli-Robson letter chart shown
in Figure 44.19 Each chart contains eight lines of six letters in two sets of three. All
letters are of the same size. Each set of three letters has a constant
contrast; however, the sets decrease in contrast by a factor of 1/ √2 or
in steps of 0.15 log units, from 100% at the top left to 0.6% at
the bottom right. Administering this test is easy, compared with
psychophysical procedures, because it more resembles an acuity test.  Fig. 44. The Pelli-Robson letter sensitivity chart. Fig. 44. The Pelli-Robson letter sensitivity chart.
|
Color Discrimination Color is classified in terms of its hue, saturation, and brightness. Hue
relates to the wavelength of the light that results in the perception
of red, green, blue, or other colors. Saturation relates to the purity
of the color, that is, how much white light is mixed with the color. Brightness
relates to the amount of luminous energy of the color. Hue
discrimination varies with the wavelength. It is greatest around 490 nm (blue-green) and 580 nm (yellow), where differences of about 1 nm
can be discriminated (Fig. 45). About 128 hues can be distinguished under good conditions. 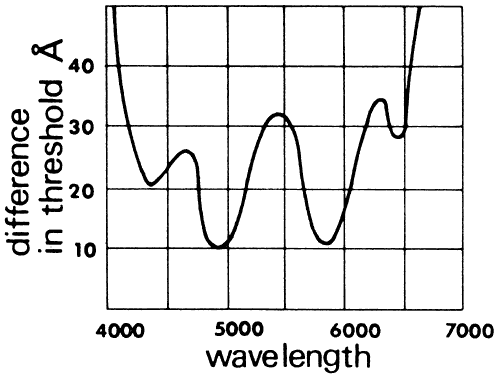 Fig. 45. Threshold sensitivity to wavelength. The smaller detectable difference
in hur is a function of wavelength. (Wulfeck JW et al: Vision in Military Aviation. WADC Technical Report 58–399. Wright
Air Development Center, OH, Nov 1959, p 115.) Fig. 45. Threshold sensitivity to wavelength. The smaller detectable difference
in hur is a function of wavelength. (Wulfeck JW et al: Vision in Military Aviation. WADC Technical Report 58–399. Wright
Air Development Center, OH, Nov 1959, p 115.)
|
SPATIAL DISCRIMINATION Minimum Visible Acuity Minimum visible acuity often is called detection and really is an example
of brightness discrimination. It is indicative of the smallest area
of the retina with which we can merely detect light without regard to
form. The quantity of light necessary, that is, the product of the area
of the fovea illuminated multiplied by the illumination, was shown
by Ricco to be a constant for angles less than 10 arc minutes. The minimum visible acuity is not determined by the size of the object
because a point source is not imaged as a point on the retina because
of aberrations and diffraction. Furthermore, fixation movements shift
the image from area to area. A point object, such as a star, can be seen
if the intensity is sufficient. Objects appear larger the higher the
intensity becomes because more retinal elements receive more than a
threshold stimulus. This explains apparent star magnitude even though
all stars are points. Stars of the sixth magnitude are the dimmest visible
in the night sky unless special precautions are taken, such as if
the observer views the night sky from a dark room through a small opening. Then
he or she may see seventh or eighth magnitude stars. This is
because it is the brightness of the sky that prevents us from seeing
these dim stars. Minimum Perceptible Acuity Minimum perceptible acuity refers to the detection of fine objects, such
as dots or lines, against a plain background. The objects may be bright
on a dark background, dark on a bright background, or of low contrast, that
is, of nearly the same luminance as their background.20 This type of acuity depends on brightness sensitivity and discrimination. The
object need not be identified, merely detected. A long black line
subtending 0.5 seconds of arc is visible against a white background. The
image of the line is diffracted and blurred over many cones instead
of being imaged as a geometric shadow of approximately 1/60 of the
cone diameter. What makes the line perceptible is that the energy on
the column of cones under the diffracted image is about 1% less than
the background energy. This is evidently the detectable difference threshold
for brightness for the given conditions. Thinner lines would produce
less than 1% reduction in illuminance on the retina and thus would
not be detected. Consequently, detecting black lines on bright backgrounds and detecting
a fine white line on a black background differ. The latter type of target
will be detected regardless of how thin it is, provided sufficient
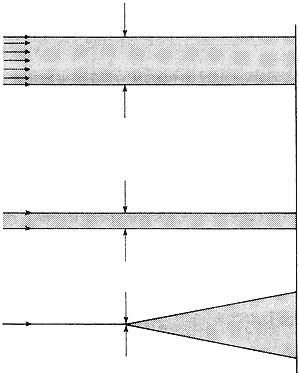
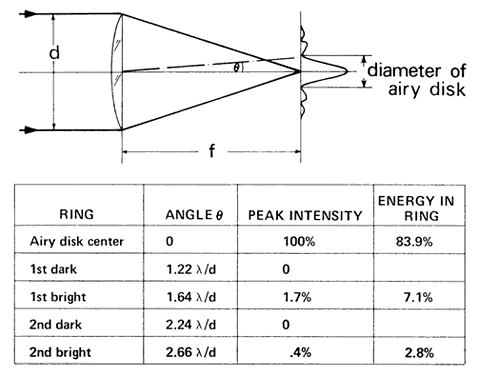
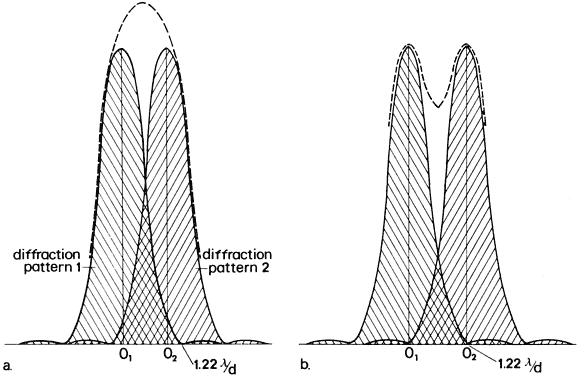
illumination reaches the retina. Minimum Separable Acuity In the section on pupillary apertures, the resolution of two diffracted
images was discussed. It was shown that when the central peak of one
pattern was superimposed on the first dark ring of the other pattern, two
sources were resolved. The angle between the sources for a 3-mm pupil
is, according to the Rayleigh limit,  = 1.22 λ/d = 0.78 minutes of arc = 0.000225 radians. For best resolution, the
expression is = 1.22 λ/d = 0.78 minutes of arc = 0.000225 radians. For best resolution, the
expression is  = λ/d = 0.64 minutes of arc = 0.000186 radians. These angles are
subtended at the nodal point of the eye and correspond to a dimension
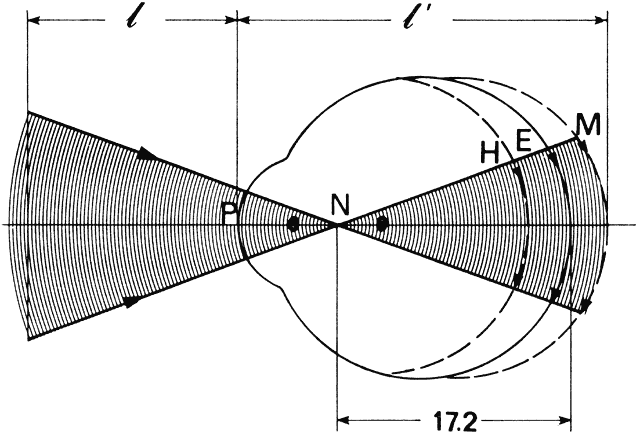
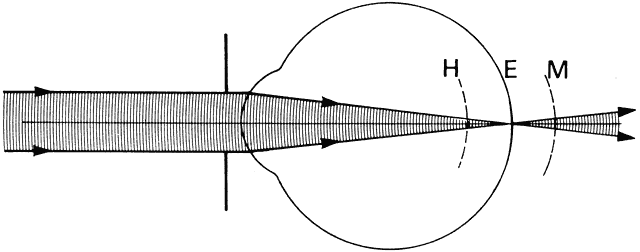
s on the retina of s = 0.000225 (17.2) = 0.0039 = 3.9 μm for the Rayleigh
limit. The smallest separation s' = 0.000186 (17.2) = 0.0032 mm = 3.2 μm. = λ/d = 0.64 minutes of arc = 0.000186 radians. These angles are
subtended at the nodal point of the eye and correspond to a dimension
s on the retina of s = 0.000225 (17.2) = 0.0039 = 3.9 μm for the Rayleigh
limit. The smallest separation s' = 0.000186 (17.2) = 0.0032 mm = 3.2 μm. Clearly, if both image patterns fell on one foveal cone, only one object
could be seen. If two adjacent cones were stimulated, there still would
appear to be one object. The necessary and sufficient condition for
resolving two objects is for two cones to be stimulated and separated
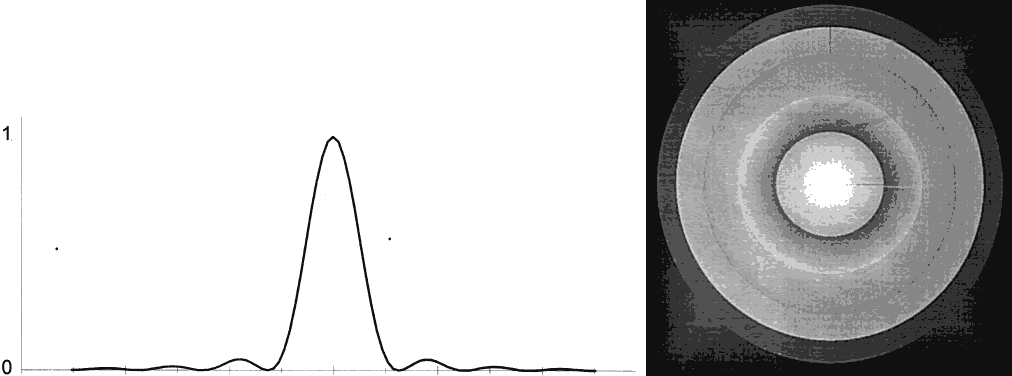
by a third cone that is subject to a perceptibly lower level of stimulation. Figure 46 illustrates how two diffraction images separated by Rayleigh's limit
would appear on the foveal cone mosaic, containing some 147,000 cones/mm2. The diameter of a cone is approximately 2 μm, and the cones are spaced 0.3 μm
apart. Cone a lies under the peak intensity of one pattern, and cone c lies under the peak of the other pattern. The reduction in intensity between
the peaks which falls on cell b is sufficient to signal the presence
of two sources. Although the diffraction patterns cover several
cones, their intensities decrease precipitously and are very low in the
outlying rings. Nevertheless, two-point resolution clearly cannot be
depicted as simply two geometric point images in cells a and c separated
by an unstimulated cell b. 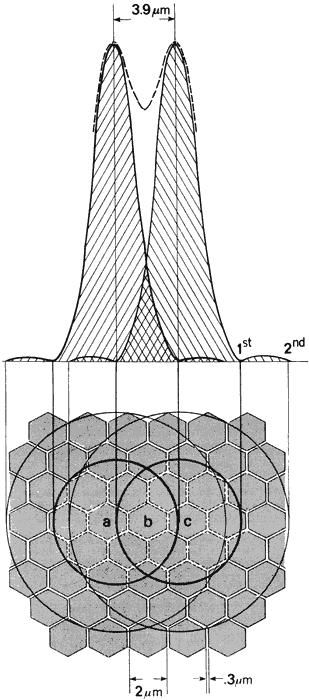 Fig. 46. Position on the retinal mosaic of diffraction patterns of two just resolvable
star images. Peaks of patterns fall on cells a and c. Cell b receives
less illumination since it corresponds to position of dip. Energy
falls off rapidly from center of patterns; however, if intensities
of the sources are very high, many more cells receive greater than threshold
stimuli; sources appear enlarged, and resolution may be lost. Fig. 46. Position on the retinal mosaic of diffraction patterns of two just resolvable
star images. Peaks of patterns fall on cells a and c. Cell b receives
less illumination since it corresponds to position of dip. Energy
falls off rapidly from center of patterns; however, if intensities
of the sources are very high, many more cells receive greater than threshold
stimuli; sources appear enlarged, and resolution may be lost.
|
Central foveal cones have diameters as small as 1.5 μm or 0.0015 mm. The
linear separation of two cones separated by a third is approximately 0.003 mm. This
corresponds to a visual angle of 
This smallest anatomically possible resolution agrees with the best practically
achieved resolution of stars. It may be concluded that the limits
to two-point resolution or minimum separable acuity are due to the
anatomy of the cone mosaic. In addition to two-point resolution, the category of minimum separable
acuity includes such tests as the Landolt C and grids of equally spaced
parallel black and white lines (Figs. 47 and 48). The gap in the C subtends one fifth of the diameter of the ring, and
the thickness of the ring is one fifth of the diameter. The position
of the gap may be rotated and the rings made progressively smaller until
the subject correctly locates the gap more than 50% of the time. Visual
acuity is defined as the reciprocal of the gap in minutes of arc. A 1-minute
gap corresponds to a standard acuity of 1. A 2-minute resolvable
gap corresponds to a visual acuity of 0.5. Figure 49 illustrates relative visual acuity as a function of the field angle from
the fovea. Figure 50 provides visual acuity as a function of background luminance for various
field angles. 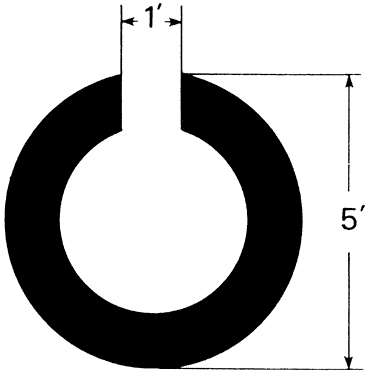 Fig. 47. Landolt C: an example of a minimum separable type test target. Fig. 47. Landolt C: an example of a minimum separable type test target.
|
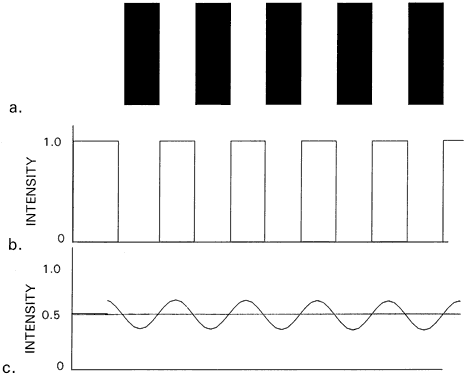 Fig. 48. a. Black-and-white square wave grating with elements subtending 0.4 minute
of arc. b. Ideal image intensity distribution. c. Actual image intensity distribution of much lower contrast. (From Schlaer S: Relation between visual acuity and illumination. J Gen
Physiol 21:165, 1937) Fig. 48. a. Black-and-white square wave grating with elements subtending 0.4 minute
of arc. b. Ideal image intensity distribution. c. Actual image intensity distribution of much lower contrast. (From Schlaer S: Relation between visual acuity and illumination. J Gen
Physiol 21:165, 1937)
|
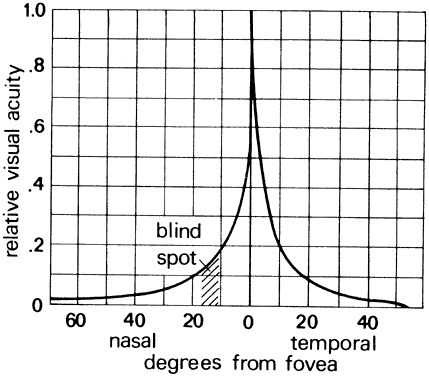 Fig. 49. Relative visual acuity as a function of field angle. Acuity is greatest
at the fovea and falls off sharply in the peripheral retina. (Chapinis A: How we see: A summary of basic principles. In: Human Factors
in Undersea Warfare. Washington, DC: National Research Council, 1949.) Fig. 49. Relative visual acuity as a function of field angle. Acuity is greatest
at the fovea and falls off sharply in the peripheral retina. (Chapinis A: How we see: A summary of basic principles. In: Human Factors
in Undersea Warfare. Washington, DC: National Research Council, 1949.)
|
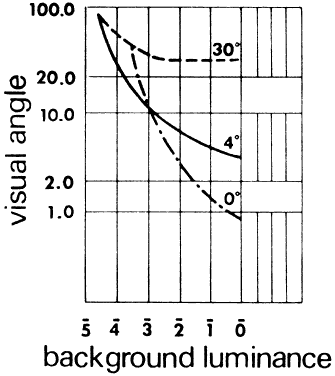 Fig. 50. Visual acuity curve. Visual angle subtended by smallest detail that can
be discriminated as a function of background luminance in log millilamberts
and image positions 0°, 4°, and 30° from the visual
axis. (Wulfeck JW et al: Vision in Military Aviation. WADC Technical Report 58–399. Wright
Air Development Center, OH, Nov 1959, p 116.) Fig. 50. Visual acuity curve. Visual angle subtended by smallest detail that can
be discriminated as a function of background luminance in log millilamberts
and image positions 0°, 4°, and 30° from the visual
axis. (Wulfeck JW et al: Vision in Military Aviation. WADC Technical Report 58–399. Wright
Air Development Center, OH, Nov 1959, p 116.)
|
Parallel line gratings of various angular subtenses provide very precise
measures of acuity and have been used to study visual acuity in humans, other
mammals, birds, reptiles, amphibians, fish, and insects. For
humans, the average angle subtended by the narrowest resolvable lines
of a grating is about 1 minute of arc or less. The reciprocal of this
angle is, again, a measure of visual acuity. Pirenne15 states that humans have a maximum visual acuity of 1.7 versus 0.017 for
the bee, or roughly 0.6 minutes versus 60 minutes for the respective
angles of resolution. As the resolution limit for a grating consisting of lines that subtend 0.4 minutes
of arc is approached, the retinal image of the bars loses
the sharpness and contrast dictated by simple geometric optics. Because
of diffraction and chromatic aberration of the eye, light from the closely
packed white image spaces spills over into the black image spaces. Instead
of the theoretical 100% white-0% black image pattern of Figure 48b, the distribution calculated by Hartridge occurs as shown in Figure 48c. The highest intensity is about 60%, and the lowest is about 40%. As noted
in the discussion on two-point resolution, there are no unstimulated
cones between stimulated cones. Instead, the central cone receives
a lower stimulus. Like the grain of photographic film, the cone mosaic
is responsible for limiting eye resolution to the angular subtense of
these narrowest cones. The limit occurs when the separation of the details
in the object results in a diffracted energy distribution at the
retina such that the difference in intensity of the middle cone is below
the threshold for perception of brightness differences. Visual Acuity and Receptive Fields Implicit in the discussion of the foveal cone mosaic is the idea that each
foveal cone is connected to the visual cortex via a single optic nerve
fiber. This, of course, is not correct. Rods and cones connect with
retinal bipolar cells, which connect with retinal ganglion cells. The
ganglion cells send fibers to the brain. These connections are highly
complicated.21 Several rods and cones form synapses with one bipolar cell, and several
bipolar cells may form synapses with one rod or cone. The connections
between the bipolar cells and the retinal ganglion cells are similarly
complicated. The mosaic of cones and rods that send signals to any particular visual
cell, either a retinal ganglion cell or a cell in the visual cortex, is
called the receptive field of the cell. Light that stimulates any portion
of the receptive field (that is any rod or cone in the receptive
field) will elicit a response in the visual cell. Various types of signals
are generated, depending on the regions of the receptive field
stimulated. Retinal ganglion cells have concentric receptive fields. The size of the
centers of these receptor fields varies greatly, but at the fovea, the
field centers are about the same size as a single cone. Thus, it is
in this sense that the foveal cone mosaic may be considered as the limiting
factor in the resolution of the eye. Strictly speaking, the limiting
factor is the mosaic of receptive fields of the foveal cones. Hyperacuity and Vernier Acuity Vernier acuity is a hyperacuity test of the ability to detect a break in
a line. It is as fine as 3 to 5 seconds of arc. That this is only a
fraction of the angular diameter of a foveal cone would appear to contradict
the statement that the cone subtense sets a lower limit to the
angle of resolution. Anderson and Weymouth22 explained this exceptional ability to detect a break in a line on the
basis of brightness differences and spatial localization. The cones above
the break in the line or edge (Fig. 51) receive a greater stimulus than those below.23 This difference is signaled by a greater frequency of nerve fiber impulses. The
displacement of the upper line from the lower extension is localized
to less than a cone diameter by a refinement of Lotze's
local signs, which states that each retinal element corresponds to a specific
direction in space (given by the line from the element through
the nodal point of the eye). An extended edge (Fig. 52) will stimulate the array of cones marked by dots. Each of these cones
corresponds to a different direction in space. The average or mean of
these directions determines the local sign of the straight line. A break
in the line causes the average local sign for the upper extension
to differ from the average local sign of the lower extension by less than
the angular diameter of a cone. By averaging the local signs of cones, localization
is not restricted to units or increments of cone diameters. Morgan24 provides a summary of hyperacuity research and theory. 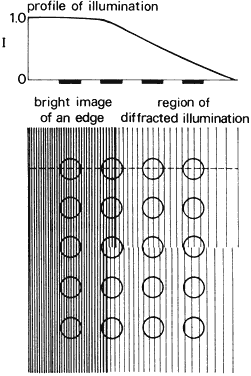 Fig. 51. Vernier acuity. Diffracted energy on the retina from the edge of a broken
line spreads out as shown by the profile of illumination, which corresponds
to a scan along the dashed line. The profile for the upper region
is slightly offset from that of the lower region; consequently, the
cones in the columns above the break in the line receive more illumination
than the cones below the break. Fig. 51. Vernier acuity. Diffracted energy on the retina from the edge of a broken
line spreads out as shown by the profile of illumination, which corresponds
to a scan along the dashed line. The profile for the upper region
is slightly offset from that of the lower region; consequently, the
cones in the columns above the break in the line receive more illumination
than the cones below the break.
|
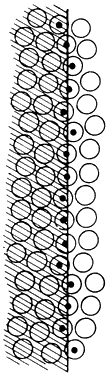 Fig. 52. The position in space of the edge of a line can be determined to less than
a cone diameter by averaging the local signs of all the cones on which
the edge of the line falls, as indicated by the cones with dots. (Adler FH: Am J Physiol 64:561, 1923.) Fig. 52. The position in space of the edge of a line can be determined to less than
a cone diameter by averaging the local signs of all the cones on which
the edge of the line falls, as indicated by the cones with dots. (Adler FH: Am J Physiol 64:561, 1923.)
|
Another form of hyperacuity test is used to evaluate vision through dense
cataracts before surgery. Enoch and coworkers,25,26 recognizing that patients with dense ocular media disorders retain the
ability to project or point to an intense light source, use three bright
sources to measure a three-point vernier acuity. Two of the sources
are aligned vertically. A source at their midpoint is randomly offset
from the vertical alignment. The patient is required to align it with
the two fixed sources. Minimum Legible Acuity In 1862, the Dutch ophthalmologist, Snellen, was the first to devise the
familiar eye chart based on findings that most emmetropes had a threshold
visual angle of 1 minute of arc for black objects on a white background. He
used black block letters to form a chart that has become the
basis for the common clinical test of visual acuity. The test requires
the identification of letters of the alphabet, the details of which
subtend certain angles at specified distances. The process of identifying letters is complicated by experience, familiarity, and
psychologic factors that permit some blur interpretation that
may be characteristic of the form of the letter. Thus, although the
Snellen test is a test of minimum separable acuity, it is not as clear
cut, for example, as resolving two points. Nevertheless, it is the clinically
preferred acuity test. The form of the Snellen letter corresponding to the 1-minute visual angle
is illustrated in Figure 53. The letter E subtends 5 × 5 arc minutes. Each bar of the letter
subtends 1 arc minute in width. When such a letter is read at a distance
of 20 feet, visual acuity is termed 20/20. This is the Snellen fraction, and
it is defined as 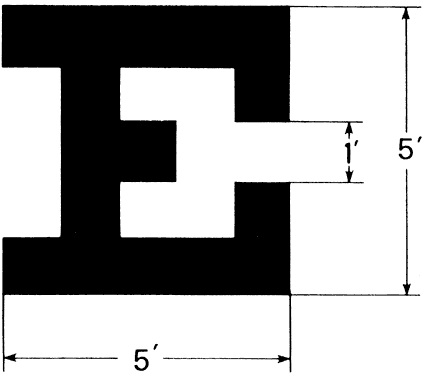 Fig. 53. Snellen E: An example of a minimum legible type test target. Fig. 53. Snellen E: An example of a minimum legible type test target.
|

Thus, 20/20 visual acuity means the subject has read a letter at 20 feet
that was designed to be read at 20 feet. A rating of 20/40 means that
a letter that normally should be read at 40 feet has to be brought to
within 20 feet before it is recognized. The normal rating of 20/20 corresponds to a visual angle of 1 minute arc
for the smallest gap in the letter; visual acuity is the reciprocal
of this angle. The visual angle for 20/40 visual acuity is 2 minutes of
arc, and visual acuity is 20 ÷ 40 = 0.5, which is called decimal
acuity. The various letters of a line of Snellen letters are not equally legible.27 The B is most difficult. It would have to be increased approximately 1.17 times
the letter E to be equally legible. The easiest letter to recognize
is the L, which to be as difficult to recognize as the E should
be reduced to approximately 0.84 times the E. In other terms, if the
ability to read a letter B that subtends 5 minutes is considered to be 20/20 visual
acuity, then the letter L can be read with an acuity as
poor as 20/30. Snellen test charts cover a range of visual acuity from 20/400 to 20/10. This
corresponds to decimal visual acuity of 0.05 to 2. The chart normally
is designed for use at 20 feet. If a chart for near vision is required, the
line corresponding to 20/20 would contain letters that subtend 5 minutes
at, for example, 16 inches, and the letters would have 1-minute
details. The American Medical Association test chart consists of 17 lines ranging
from 20/20 to 20/200. The lines of this chart are designated additionally
with a value termed visual efficiency. This is an arbitrary rating evidently used as a basis for industrial
compensation for vision impairment. Because the 17 lines are designed
in 5% steps of visual efficiency from 100% to 20%, the equivalent Snellen
rating is not a round number (Fig. 54). 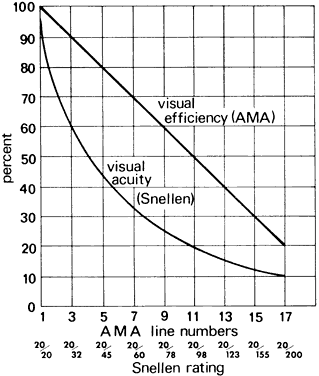 Fig. 54. Comparison of visual efficiency and acuity. Fig. 54. Comparison of visual efficiency and acuity.
|
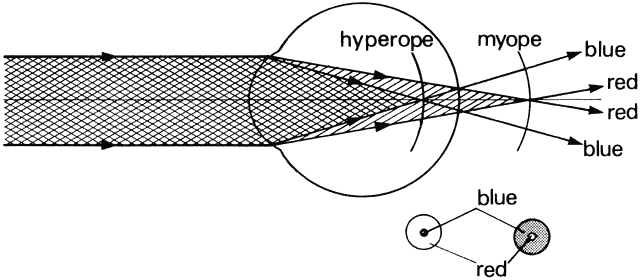
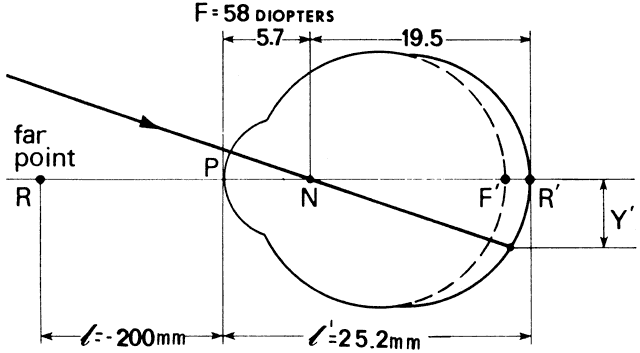
Figure 55 illustrates the relationship between Snellen visual acuity and refractive
error for myopes and hyperopes. A 1-D refractive error reduces visual
acuity to 20/50 for both ametropes. 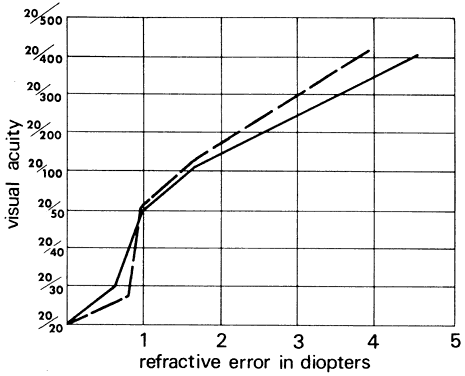 Fig. 55. Visual acuity as a function of refractive error. Solid line corresponds
to absolute hyperopia; dashed line corresponds to myopia. (Wulfeck JW, et al: Vision in Military Aviation. WADC Technical Report 58–399. Wright
Air Development Center, OH, Nov 1959, p 55.) Fig. 55. Visual acuity as a function of refractive error. Solid line corresponds
to absolute hyperopia; dashed line corresponds to myopia. (Wulfeck JW, et al: Vision in Military Aviation. WADC Technical Report 58–399. Wright
Air Development Center, OH, Nov 1959, p 55.)
|
Bailey-Lovie Chart The Bailey-Lovie28 chart, shown in Figure 56, was designed to overcome deficiencies in the Snellen chart. It has the
following design features. All letters are of almost equal legibility
and constructed with a 5 × 4 format. At 20 feet, their stroke
widths or the angles of resolution of the letters go from 10 to 0.5 minutes
of arc, corresponding to an acuity range from 20/200 to 20/10.  Fig. 56. The Bailey-Lovie test chart. Fig. 56. The Bailey-Lovie test chart.
|
Each line contains five letters, with between-letter spacing equal to the
width of a letter to avoid crowding. The between-line spacing above
a line is equal to the height of the letters in that line. The 14 lines
of letters progress in size geometrically in a ratio of 10 √ 10, or 0.1 log
units. Each correctly identified letter on a line of five
letters is scored at 0.02 log units. The LogMAR Scale Visual acuity is expressed as the logarithm of the minimum angle of resolution
or logMAR.28 This is the log10 of the stroke width at 20 feet. Table 5 shows the equivalence of logMAR, Snellen, and decimal acuity scales. Also
shown is the corresponding angular resolution of a black-and-white
line pair. A 20/20 letter subtends 5 minutes of arc. It has a line stroke
of 1 minute of arc. A black-and-white line stroke subtend 2 minutes
of arc. The decimal equivalent of 20/20 = 1. Because the log10 1 = 0, the logMAR value = 0. A 20/200 letter has a line stroke of 10 minutes
of arc. Its logMAR value is 1 because log10 10 = 1. TABLE 5. Visual Acuity Scales
| LogMar | Snellen | Decimal | Resolution Angle (min of arc) |
| 1.0 | 20/200 | 0.10 | 20.00 |
| 0.9 | 20/160 | 0.13 | 16.00 |
| 0.8 | 20/125 | 0.16 | 12.50 |
| 0.7 | 20/100 | 0.20 | 10.00 |
| 0.6 | 20/80 | 0.25 | 8.00 |
| 0.5 | 20/63 | 0.32 | 6.30 |
| 0.4 | 20/50 | 0.40 | 5.00 |
| 0.3 | 20/40 | 0.50 | 4.00 |
| 0.2 | 20/32 | 0.63 | 3.20 |
| 0.1 | 20/25 | 0.80 | 2.50 |
| 0.0 | 20/20 | 1.00 | 2.00 |
| -0.1 | 20/16 | 1.25 | 1.60 |
| -0.2 | 20/12.5 | 1.60 | 1.20 |
| -0.3 | 20/10 | 2.00 | 1.00 | If it is necessary to test at less than 20 feet, the logMAR score of the
lowest legible line is corrected by adding the log10 (20/test distance). For example, if the chart distance is 4 feet, log10 20/4 = 0.7, and if the lowest legible line has a logMAR value of 0.5 (20/63), the
total logMAR value is 1.2. This means that the line stroke
is 101.2 = 15.85 minutes of arc. Because 1 minute of arc corresponds to 20/20, the
denominator of the Snellen fraction will be 20 × 15.85 = 317. Rounding
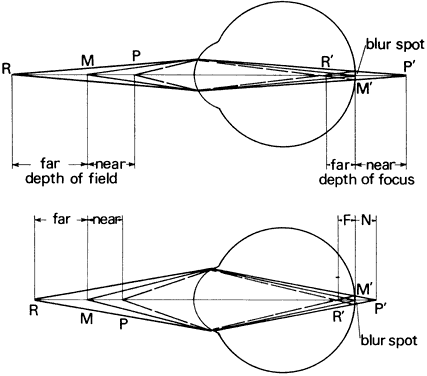
will result in a visual acuity of 20/320. DISTANCE DISCRIMINATION Depth perception may be an estimate of the distance an object is from the
observer or a discrimination between the relative distances of two
or more objects, particularly which is nearer or farther. Many monocular
cues to distance judgments have been learned from experience. These
cues frequently are pictorial, such as perspective, light and shadow, overlapping
contours, and aerial perspective. Motion parallax, which
we may observe from a moving vehicle, will cause near objects to appear
to move oppositely when fixating at far, and vice versa. The two binocular cues to distance judgment are convergence of the eyes
and stereopsis. Convergence requires muscular action, which poorly provides
an indication of the distance of an object. Stereoscopic vision
provides a very sensitive cue to depth at near ranges. Approximately 64 mm
separate the two eyes, consequently, they receive slightly different
views of an object. This creates a retinal disparity that the brain
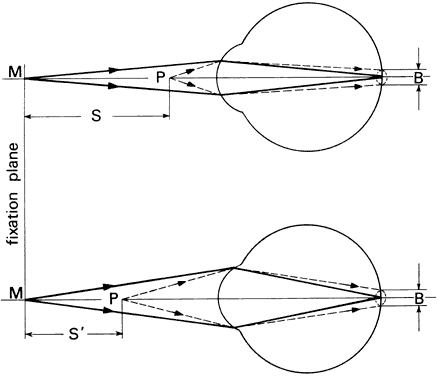
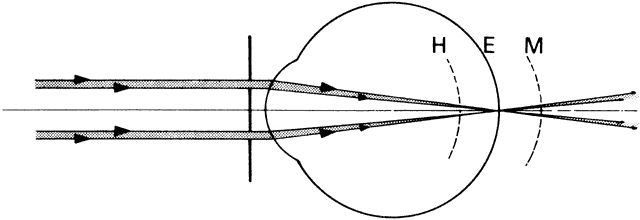
interprets as solidity or depth. If the eyes fixate point M in Figure 57, its image will fall on the fovea of each eye. The images of the more
distant point P will fall nasally to the fovea of both eyes. The regions
of the retinas that the P images stimulate are not corresponding; however, if
the disparity is less than 20 minutes of arc, the P images
lie within Panum's area and we will see P as a single point. If the
disparity exceeds Panum's area, the more distant point P will
appear double when we fixate point M. The right eye will see an image
of P to the right of point M and the left eye will see an image of P to
the left of point M. We call this uncrossed diplopia. If we shift the
fixation point to point P, which is farther than point M, the images
of M will appear double when they fall outside Panum's area. In
this instance, the doubled images of M will appear crossed. The right
eye will see point M to the left of P and the left eye will see point
M to the right of P. Retinal disparity decreases with increasing object
distance, and beyond about 2000 feet stereoscopic judgments are of little
value. 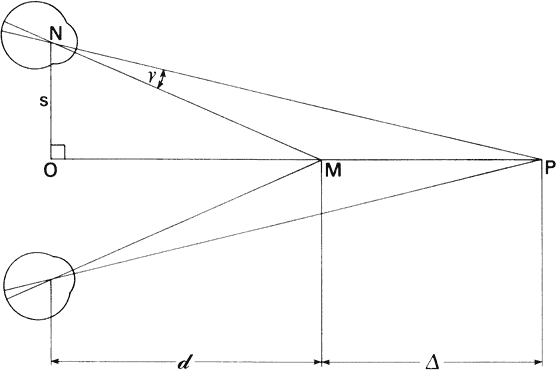 Fig. 57. Stereoscopic acuity. The ability to distinguish depth depends on angle. Fig. 57. Stereoscopic acuity. The ability to distinguish depth depends on angle.
|
Figure 57 illustrates the geometry of stereoscopic depth perception. The eyes are
fixating point M at distance d. Point P at some slightly different distance
forms an angle γ at the nodal point of the eye with respect
to point M. Angle γ is the angle of depth discrimination. Values
of γ as low as 2 seconds of arc have been reported. Stereoscopic
depth discrimination, like vernier acuity, is less than the subtense
of a cone and is explained similarly. | 
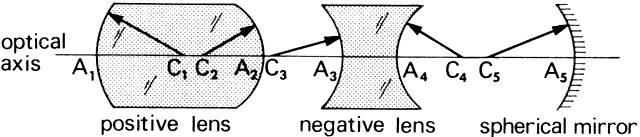
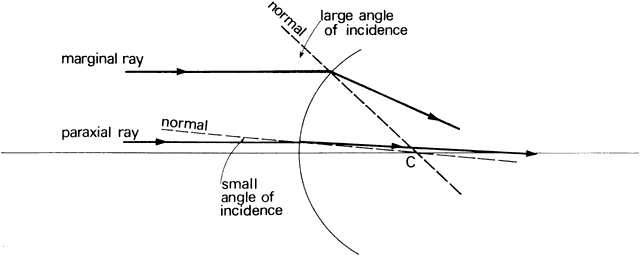

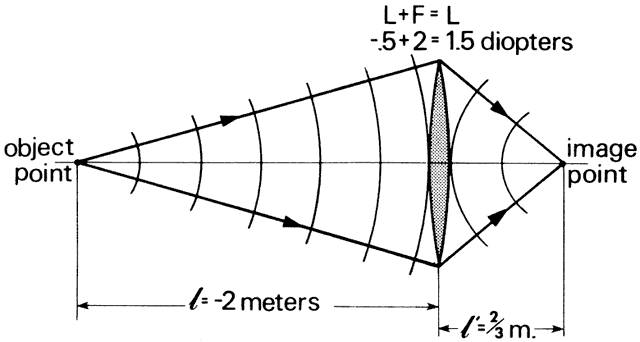
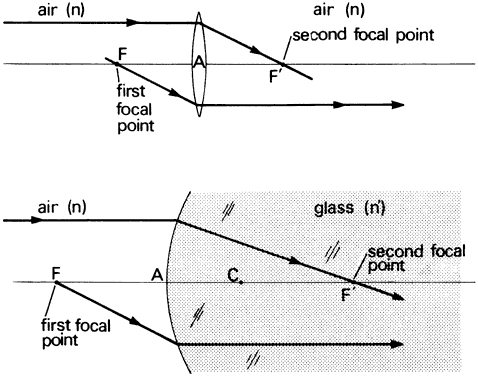
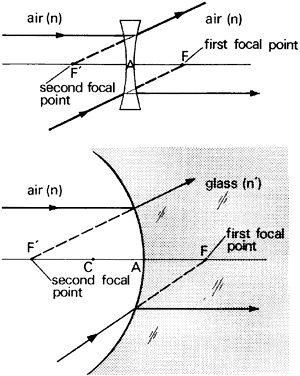
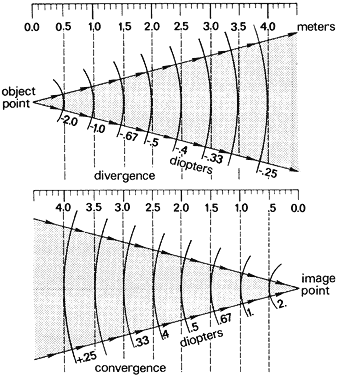
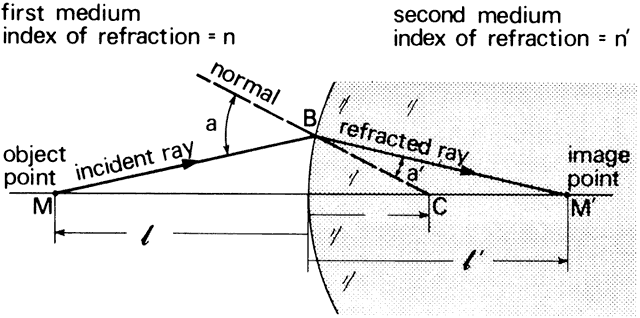
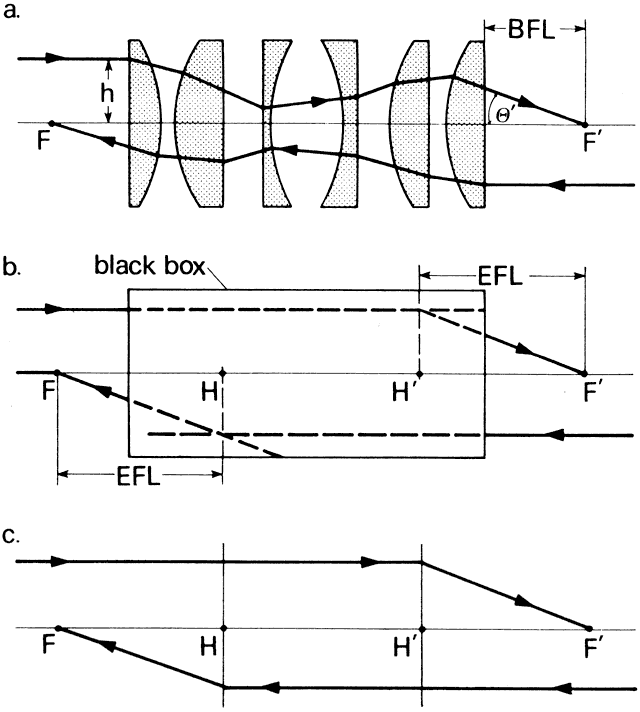
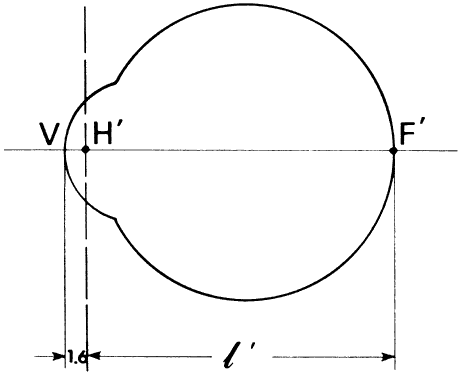
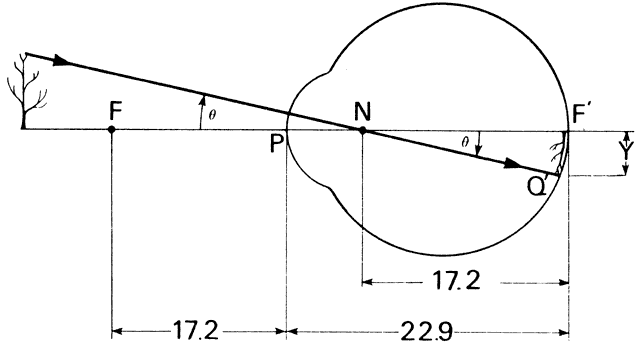
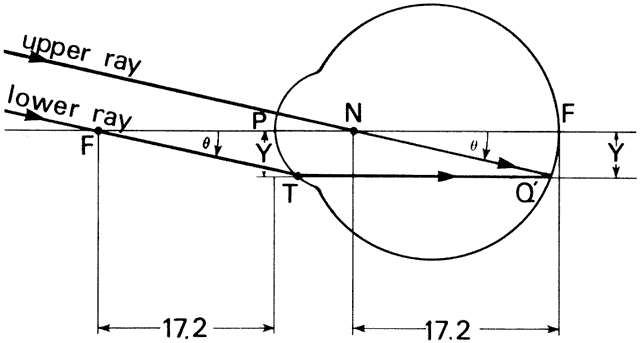
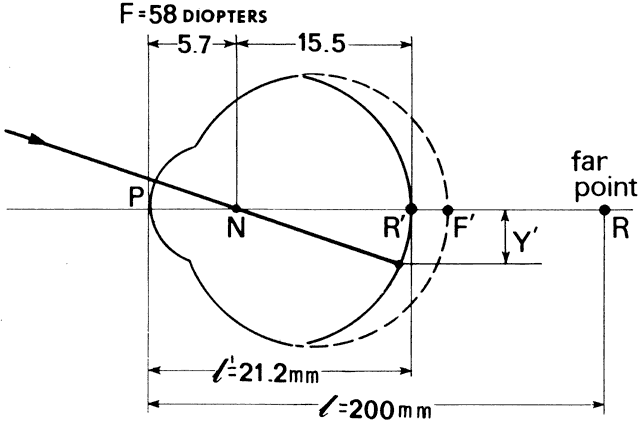
 ' toward the focal point of a paraxial incident ray are known. The second
principal plane is located by extending the incident ray forward and
the emerging ray backward until they intersect. This plane defines the
position of a thin lens that theoretically could replace the lens system. The
point H' where this plane crosses the axis is called the second
principal point. The distance from F' to H' is the equivalent focal
length of the complex lens.
' toward the focal point of a paraxial incident ray are known. The second
principal plane is located by extending the incident ray forward and
the emerging ray backward until they intersect. This plane defines the
position of a thin lens that theoretically could replace the lens system. The
point H' where this plane crosses the axis is called the second
principal point. The distance from F' to H' is the equivalent focal
length of the complex lens.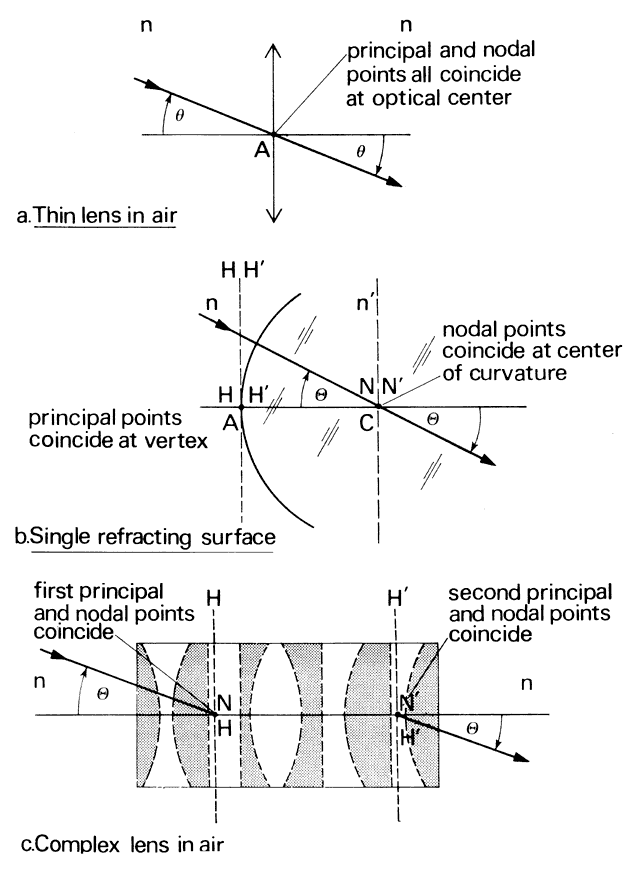
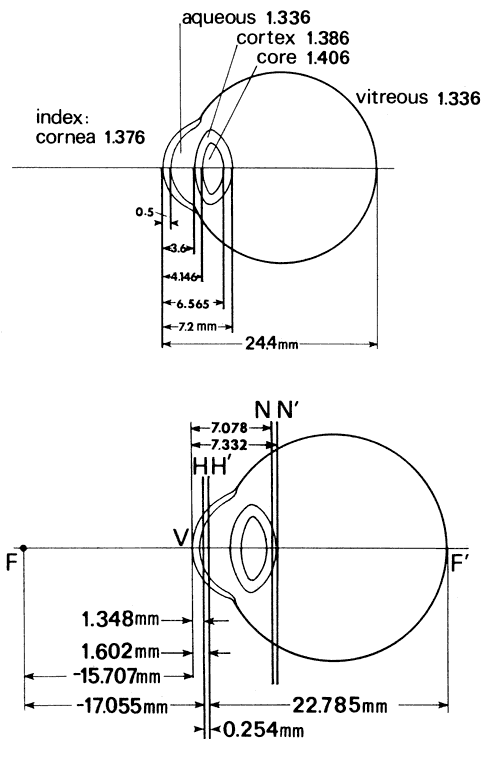


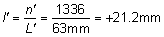
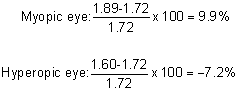
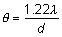
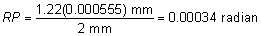
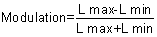
 63 cpd. Dividing 63 cpd into 600 converts it into
63 cpd. Dividing 63 cpd into 600 converts it into