| There are four important aberrations which affect vision through spherical
and toric ophthalmic lenses: (1) Chromatic aberration, in which the
dispersion of light into its various colors by a lens is inherent in
the nature of the refracting material and of the light itself. The most
that can be done with ophthalmic lenses to reduce chromatic aberration
is to utilize refracting material having a low dispersive quality. (2) Curvature
of the field, in which there is excessive spherical refractive
power in the lens for lateral gaze through it. (3) Marginal astigmatism, in
which there is astigmatism in oblique gaze through lateral
portions of the lens. (4) Distortion, in which there is nonuniformmagnification
of the field of vision through the lens. The monochromatic blurring aberrations, curvature of the field, and marginal
astigmatism, in both spherical and toric lenses, are reduced by
appropriate bending of the lens, ie, the relative curvatures of the two
surfaces of the lens, known as coflexure. Corrected curve spherical
and toric lenses which permit the widest and clearest field of vision
depend on specific coflexures for specific powers of the lenses to minimize
the blurring aberrations. The appropriate coflexure also reduces
distortion but does not eliminate it. The correction of aberrations of spherical lenses by coflexure is quite
effective for minus power lenses as strong as -20.00 D and for plus power
lenses up to +7.50 D. For lens powers above +7.50 D, aberrations
cannot be reduced satisfactorily by coflexure. Excessive lateral
power and lateral astigmatism can be corrected only by gradually
changing the curvature of one of the surfaces of the spectacle lens, usually
the anterior surface. By a continuous and regular reduction in
curvature from the apex of the front surface to its periphery, both lateral
power excess and lateral astigmatism are reduced. Such a surface
is shaped like the end of an oval or egg, ie, ellipsoidal. Strong plus
power lenses such as cataract lenses which have ellipsoidal front surfaces
combined with spherical or toric back surfaces are far superior
to spherical and toric lenses of the same back vertex power: the field
of vision for given size lenses is somewhat larger in the aspheric lenses
due to the more uniform magnification, and vision is considerably
clearer throughout the field. The grinding technique used for spherical lenses cannot be applied to
aspheric lenses. Although it rotates about its own axis during the grinding
and polishing, the spherical lens moves with respect to the axis
of the grinding tool so that the lens and tool axes do not coincide and
are continually changing their angular relationship with respect to
each other. In the grinding procedure, broad areas of the rotating grinding
tool and the rotating lens are in contact and precise surfaces
are obtained. In the grinding of aspheric surfaces other than toric surfaces, only
limited areas of the surface of the grinding tool can be
in contact with the lens surface; it is difficult to produce and maintain
the desired surface contour of an aspheric lens throughout the grinding
and polishing procedures. Various techniques are utilized to overcome
the difficulties in the production of aspheric surfaces. All aspheric
lenses other than toric lenses are high in cost as compared with
spherical lenses, and it is the cost which has limited the use of aspheric
ophthalmic lenses. THE CORNEA The anterior surface of the human cornea closely resembles an ellipsoid, ie, highly
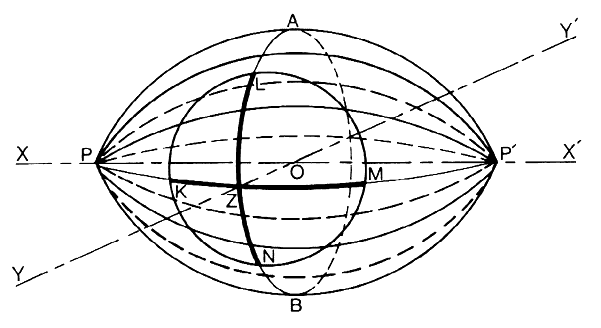
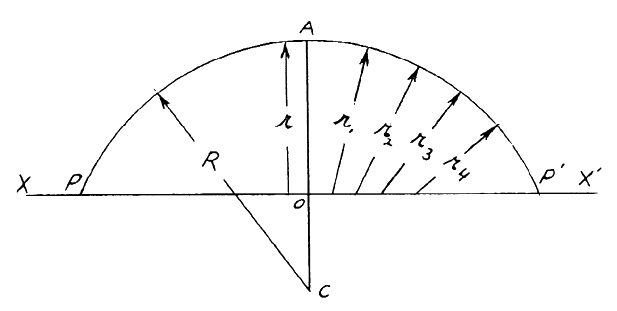
curved centrally and flattening toward the periphery (Fig 1). The central area of the anterior surface of the cornea may be free of
astigmatism, resembling a spherical surface, while the remainder of
the cornea becomes increasingly flat and astigmatic peripherally. The
central, practically spherical, area subserves central vision; such a
cornea is said to be free of astigmatism. 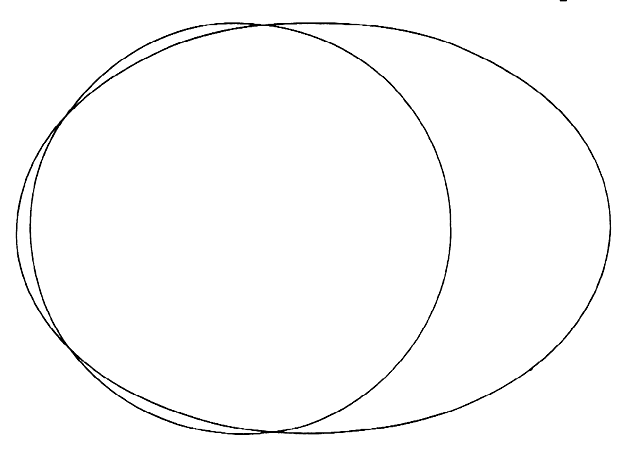 Fig 1. Schematic scale representation of a section through an ellipsoidal cornea. Entire
ellipse illustrates relationship between end of ellipse serving
as model for section of anterior corneal surface and circular section
representing the sclera. Fig 1. Schematic scale representation of a section through an ellipsoidal cornea. Entire
ellipse illustrates relationship between end of ellipse serving
as model for section of anterior corneal surface and circular section
representing the sclera.
|
Alternatively, the central area may resemble a toric surface; such a cornea
is said to be astigmatic, regardless of the peripheral portions of
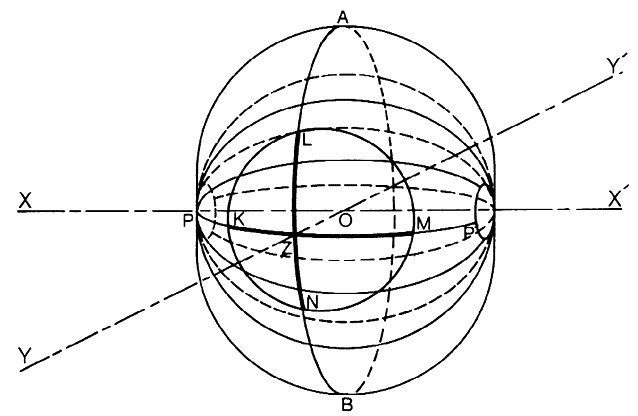
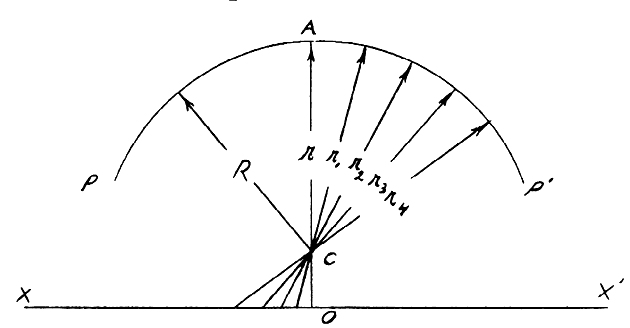
the cornea. An idealized version of a principal section of the anterior corneal surface
is shown in Figure 2, wherein a spherical surface of a specific radius of curvature matches
or “osculates” the central area of the ellipsoidal cornea. The
two surfaces appear to be in contact over a relatively large central
area.  Fig 2. A circular section osculating an elliptical section at apex of ellipse. Radius
of curvature of circle is equal to apical radius of curvature
of ellipse. Fig 2. A circular section osculating an elliptical section at apex of ellipse. Radius
of curvature of circle is equal to apical radius of curvature
of ellipse.
|
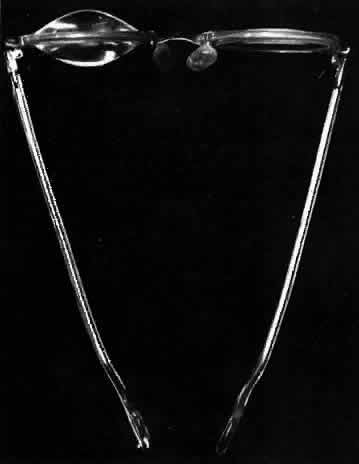
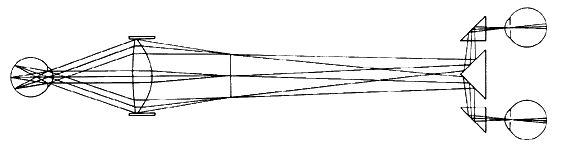
The simplest instrument for studying the corneal contour is a keratoscope, such
as the Placido's disc (Fig 3), which consists of a circular target with alternate black and white annuli
and a handle. Usually a +5.00-D lens is placed behind an aperture
in the center of the disc to enable the examiner to see the image
of the target produced by specular reflection from the smooth tear
film overlying the cornea. The target, either illuminated indirectly or
self-luminous, has an image formed of it by the cornea which is observed
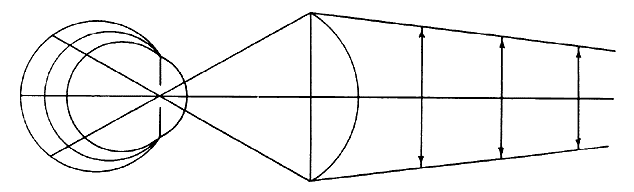
through the lens of the instrument. Figure 4 illustrates the appearance of the central corneal image of the target
when there is no central astigmatism; the image consists of a series of
successively larger circular white rings centered about the corneal
apex. Figure 5 demonstrates the appearance of the image of the target as produced by
the astigmatic periphery of the cornea. When the central cornea is astigmatic
the images of the target rings are elliptic, with the long axis
of each of the ellipses along the flatter meridian of the cornea.  Fig 3. Placido"s disc, a keratoscope. Fig 3. Placido"s disc, a keratoscope.
|
 Fig 4. Representation of image of annuli of keratoscope target as formed by central
portion of cornea which is free of astigmatism. Fig 4. Representation of image of annuli of keratoscope target as formed by central
portion of cornea which is free of astigmatism.
|
 Fig 5. Representation of image of annuli of keratoscope as formed by astigmatic
peripheral portion of cornea. Fig 5. Representation of image of annuli of keratoscope as formed by astigmatic
peripheral portion of cornea.
|
|