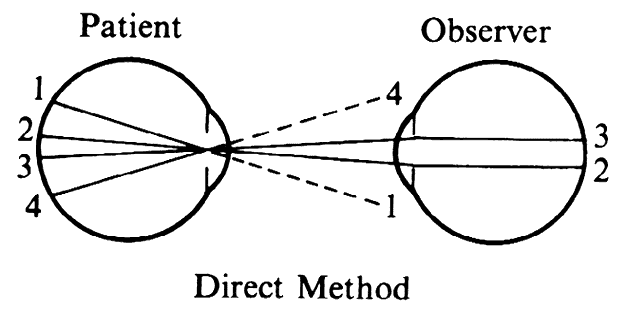
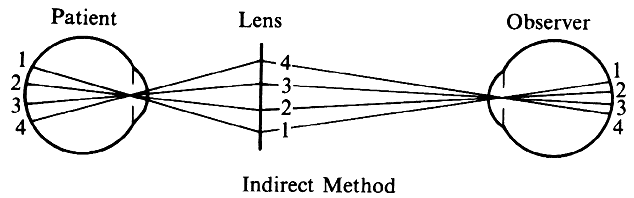
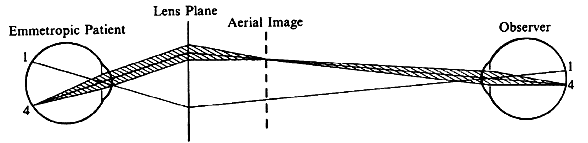
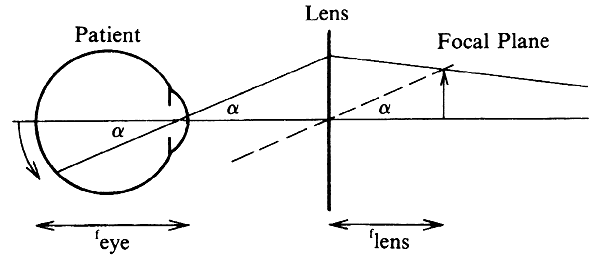
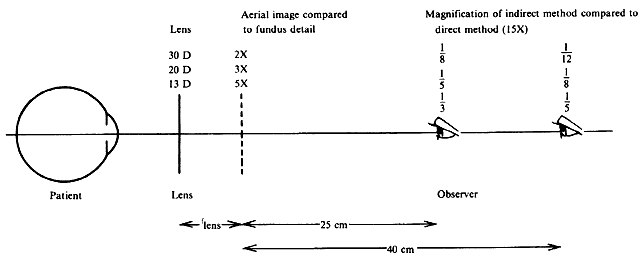
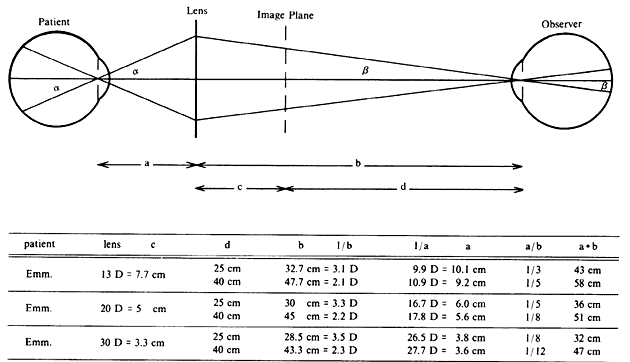
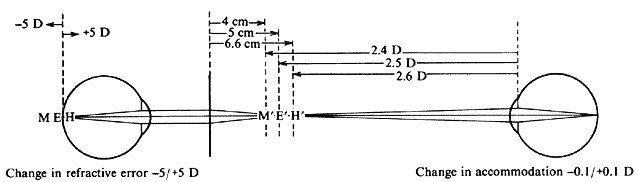
| Although not generally considered as a method of ophthalmoscopy, fundus
examination with the slit lamp offers an important addition to the traditional
methods of direct and indirect ophthalmoscopy. It offers the
advantage of high-power magnification through the microscope and flexible
illumination with the slit-lamp beam. With appropriate contact lenses, it
can offer higher magnification than direct ophthalmoscopy and
a field several times wider than indirect ophthalmoscopy. These methods
have become particularly important in combination with laser treatment. Because the slit-lamp microscope has a fixed focus on a plane approximately 10 cm
in front of the objective and because the image of the fundus
of an emmetropic eye appears at infinity, the fundus cannot be visualized
without the help of additional lenses. There are several options. NEGATIVE LENS A negative lens placed in front of the objective of the microscope can
move the microscope focus to infinity. The practical application of this
principle was worked out by Hruby19,20 of Vienna (1942) with a lens known as the Hruby lens. The optical principle is best understood if the lens is considered in conjunction
with the eye, rather than as a part of the microscope. Parallel
rays emerging from an emmetropic eye are made divergent by the Hruby
lens and seem to arise from the posterior focal plane of that lens (Fig. 23A). For a -50-D lens, this would be 20 mm behind the lens (the usual Hruby
lens is -55 D). The slit-lamp microscope is thus looking at a virtual
image of the fundus in a plane somewhere in the anterior segment and
must be moved a little closer to the patient than it would be for the
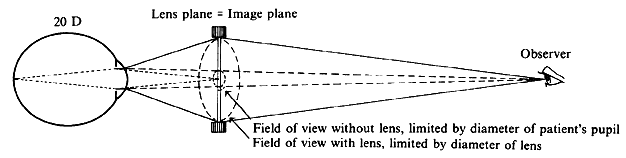
regular external examination. 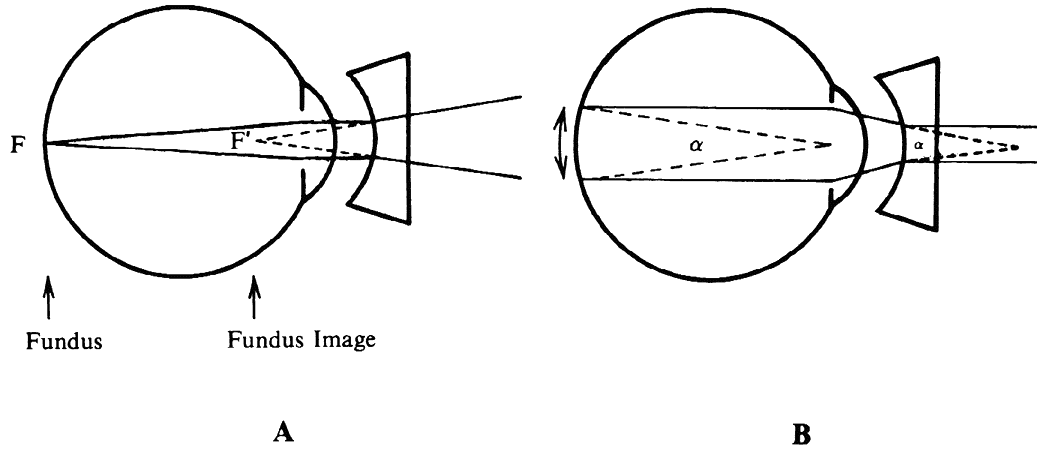 Fig. 23. Hruby lens. A. The fundus image (F') is formed in the posterior focal plane of the lens. B. The field of view is proportional to the size of the pupil as seen from
the anterior focal point of the lens. Fig. 23. Hruby lens. A. The fundus image (F') is formed in the posterior focal plane of the lens. B. The field of view is proportional to the size of the pupil as seen from
the anterior focal point of the lens.
|
To estimate the field of view in this method, it may be assumed that only
rays emerging parallel to the axis will reach the objective of the
microscope and the observer's eye. When emerging from the eye, these
rays must have been aimed at the anterior focal point of the Hruby
lens. Fig. 23B, in which these rays are traced back to the retina, shows that the field
of view (a) is proportional to the pupillary diameter as seen from
the anterior focal point of the lens. This field is of the same order
of magnitude as the field in direct ophthalmoscopy; it is largest when
the lens is closest to the eye. With the lens close to the cornea, the fundus image will be close to the
fundus plane and approximately actual size. The magnification to the
observer is thus largely determined by the magnification of the microscope. At 16×, the
magnification is about equal to that of direct
ophthalmoscopy; at higher settings, the magnification is greater. Binocular
viewing and slit illumination are advantages over direct ophthalmoscopy, even
at similar magnification. Limitation to the posterior
pole is a disadvantage. CONTACT LENS When the Hruby lens is moved progressively closer to the eye, it will eventually
touch the cornea and become a contact lens. If the curvature
of the posterior lens surface equals the curvature of the anterior corneal
surface, the image formation will not change, but two reflecting
surfaces will be eliminated, and image clarity will increase. The use of a contact lens for fundus examination was perfected by Goldmann21 of Berne, Switzerland (1938). His contact lens is known for the three
mirrors incorporated in it. These mirrors positioned at different angles
make it possible to examine the peripheral retina with little manipulation
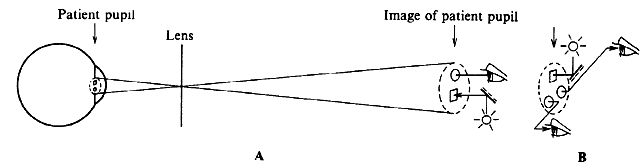
of the patient's eye or of the microscope axis (Fig. 24). 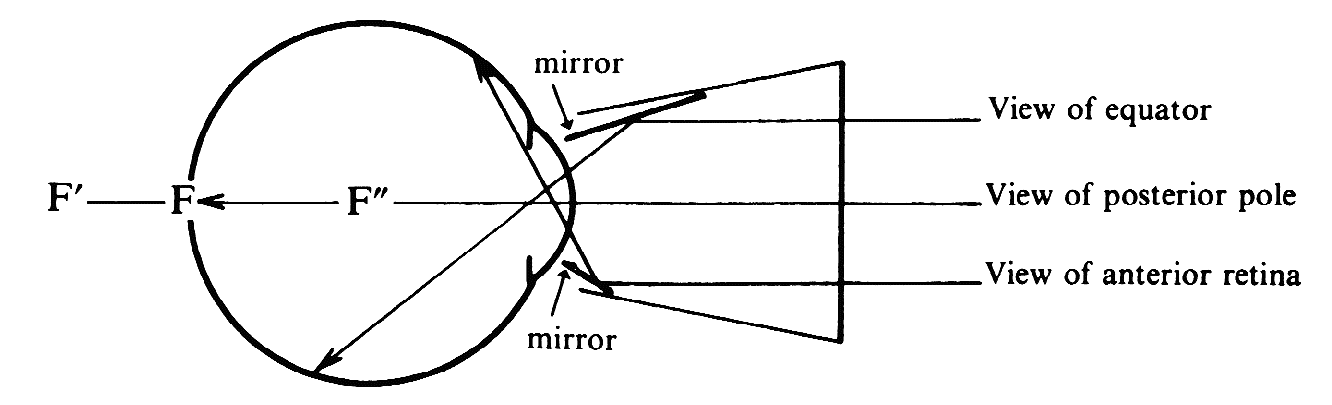 Fig. 24. Three mirror contact lens by Goldmann. Two of the three mirrors are shown. They
allow visualization of different parts of the fundus. Fig. 24. Three mirror contact lens by Goldmann. Two of the three mirrors are shown. They
allow visualization of different parts of the fundus.
|
The refractive power of the cornea is eliminated in the contact lens. The
only effective refractive element left would seem to be the far less
powerful crystalline lens. The retina is situated well within the focal
length of this lens, and the crystalline lens will therefore form
a virtual image of the fundus (F) in a plane (F') behind the globe. How
can the microscope focus on an image that far back? We overlooked one
other refracting surface: the plano front surface of the contact lens. F' is
seen through plastic and vitreous. To the observer in air F' appears
at F", through the same effect that makes a swimming pool appear
shallower than it is. Because of this, the microscope again must focus
on a plane inside the globe. As with the Hruby lens, magnification
is largely determined by the microscope. Thus, contact lens fundus microscopy extends our range of examination methods
to details beyond the reach of ordinary direct ophthalmoscopy. “INDIRECT” SLIT-LAMP MICROSCOPY The use of the Hruby lens and Goldmann contact lens is comparable to direct
ophthalmoscopy, because no real intermediate image is formed. The
equivalent of indirect ophthalmoscopy can be achieved by focusing the
microscope on the real image formed by a high-power plus lens. El Bayadi22 introduced the use of a +60-D lens for this purpose. The inverted
image formed by this lens is situated 16 mm (0.0167 m) in front of it. A
practical problem with some older slit lamps is that they cannot be
pulled back far enough to observe this image. Compared with the Hruby (-55 D) lens, the El Bayadi (+60 D) lens offers
the same major advantage as does indirect ophthalmoscopy: a larger
field of view. With proper placement of the lens, the field is about
six disc diameters (40 degrees), compared with the one- or two-disc
diameter field of the Hruby lens. With a 60-D lens the aerial image is as large as the fundus; thus the magnification
is approximately equal to the microscope magnification (similar
to that with the Hruby lens). CONTACT LENS FOR THE INDIRECT METHOD Can the field of view be widened even further? This is possible by using
a contact lens of very high plus power with some additional optical
tricks. Figure 25 illustrates the Rodenstock Panfunduscope, based on a design by Schiegel.23 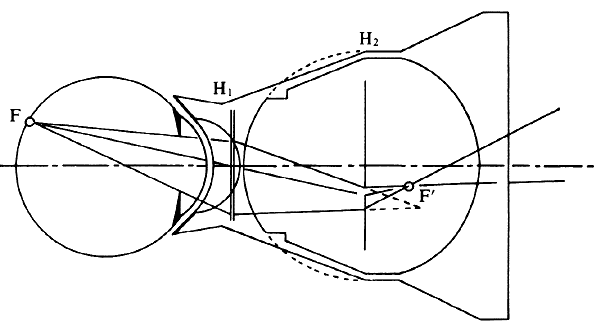 Fig. 25. Contact lens arrangement for wide-angle indirect biomicroscopy. A high-power
contact lens forms an inverted image (F') inside a spherical element, which
redirects the light toward the observer. Fig. 25. Contact lens arrangement for wide-angle indirect biomicroscopy. A high-power
contact lens forms an inverted image (F') inside a spherical element, which
redirects the light toward the observer.
|
The unit contains a high plus contact lens, which forms an inverted fundus
image (F') located inside a second, spherical glass element. In this arrangement, as in the previous example of a high myope (see Fig. 13), the image-forming and field-widening functions of the ophthalmoscopy
lens are separated again. The contact lens forms the image; the spherical
element serves to flatten the image and to redirect the diverging
pencils of rays toward the observer. Because these elements are so close
to the eye, the field of view can be very wide. Indeed, without moving
the lens, the view reaches 200 degrees, that is, from equator to
equator, 4 to 5 times the diameter (16 times the area) of regular indirect
ophthalmoscopy or of the El Bayadi lens. The size of the image inside the front lens is 70% of the retinal size; for
detailed examination, therefore, 50% more microscope magnification
is required than with the other slit-lamp methods. However, the principal
use of this lens is not for its magnification but for its overview, an
overview previously achievable only in fundus drawings or photocompositions. Similar contact lens arrangements are used in specially designed fundus
cameras that allow fundus photography of areas 100 degrees or more in
diameter. With lenses such as these, the spectrum of our examining methods
can be extended not only toward higher magnification than with direct
ophthalmoscopy but also, at the other end, toward an overview of
the fundus considerably beyond that obtainable with regular indirect
ophthalmoscopy. As the technology to calculate, design, and manufacture lenses with aspheric
surfaces has improved, it has been possible to make lenses with
higher powers and better light gathering abilities. The number and variety
of lenses for indirect ophthalmoscopy and of contact lenses for slit-lamp
microscopy has grown accordingly. RELATED IMAGING TECHNIQUES Several related techniques to produce retinal images will be discussed
briefly. Fundus Photography Fundus cameras have greatly improved the ability to document and follow
fundus lesions. Eduard von Jaeger often spent countless hours drawing
a single fundus, but today a photographic image is available in a fraction
of a second. For reasons mentioned earlier, fundus cameras are built
on the principle of indirect ophthalmoscopy. The observer's
lens and retina are replaced by a camera lens and film. Because all components
are enclosed in a rigid housing, more accessories can be built
in. This includes a dual illumination system, which includes a constant
light source for focusing and a flash for photography, and filters
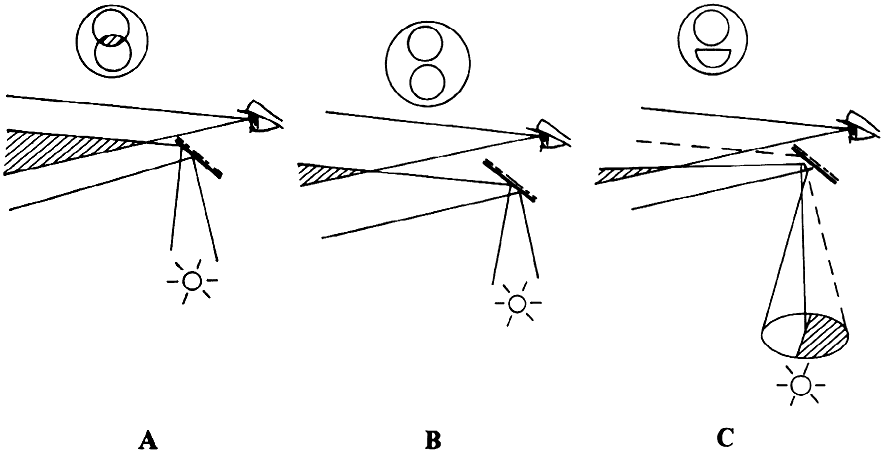
such as for fluorescein angiography. Rather than placing the viewing
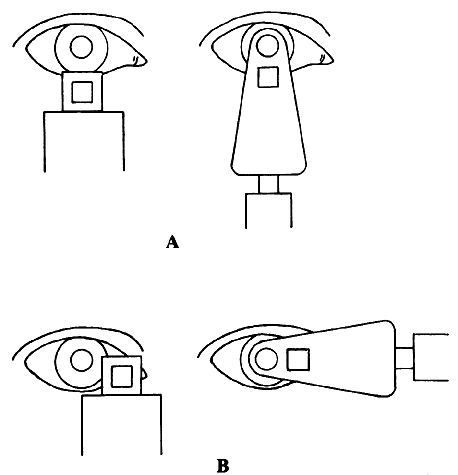
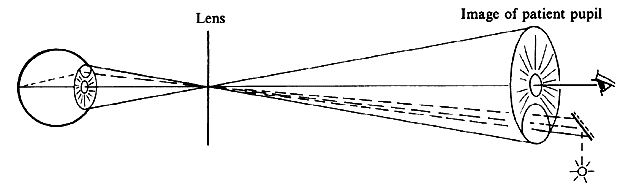
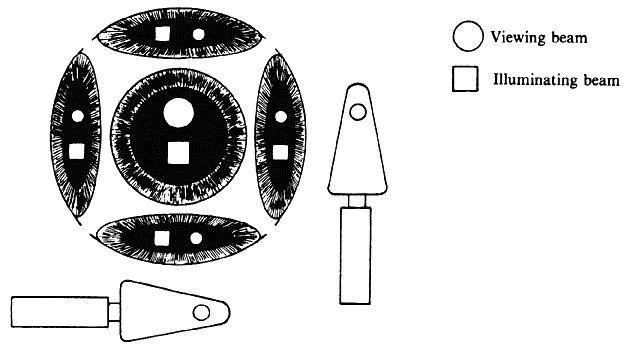
and illumination beams side by side, the illumination beam generally uses
the periphery of the pupil and leaves the center for the observation
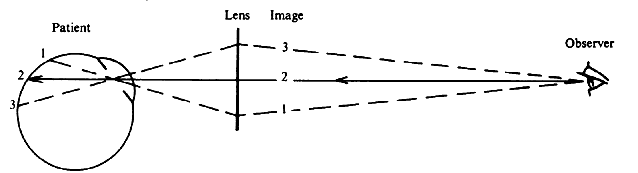
beam.24 An angled glass plate that can be flipped to the right or to the left can
be used to slightly deviate the observation beam to the right part
or the left part of the patient's pupil to produce photo pairs that
can be viewed stereoscopically. Because newer lens designs have allowed the construction of wide-angle
cameras, a special challenge has been to construct the optical system
in such a way that the curved retina is imaged in a plane that can be
captured on a flat film. Adaptive Optics The optics of the eye are not perfect. Even if major errors are corrected
with spherical and cylindrical lenses, small irregularities across
the pupillary opening persist. The technique of adaptive optics was developed
for astronomical telescopes to counteract image degradation by
atmospheric irregularities. An adaptive optics system uses a grid to
divide the pupillary opening into many small areas and determines a separate
small correction for each area. The information is fed to a slightly
deformable mirror with microactuators. Thus the image quality can
be enhanced to the point at which the cone mosaic can be clearly visible. The
setup is too laborious for use in routine photography. Because
the corrective system has to be fixed in relation to the pupil, it
cannot be implemented in glasses or contact lenses. However, the technique, also
known as wavefront analysis, has found a place in the refractive
sculpting of the cornea.25 Digital Imaging The advent of digital cameras has replaced the use of film in many applications. The
advantages include easier storage and manipulation, as well
as greater sensitivity, so that less light can be used or fainter
images can be captured. Scanning Laser Ophthalmoscope (SLO) This device takes the advantages of digital imaging one step further. In
conventional photography all points of the object are illuminated and
imaged onto corresponding points of the film simultaneously. In the
Scanning Laser Ophthalmoscope (SLO) the points on the retina are illuminated
sequentially by a scanning laser beam; the diffusely reflected
light is not imaged but collected on a photocell that can collect light
from the entire pupillary area. This allows another significant increase
in light sensitivity. In this process the topographic information
is transformed into a sequential modulation of signals over time. The
image information is recovered by feeding the signals to a video monitor, in
which the beam moves in the same way as did the scanning beam.26 An interesting application results from the fact that the illuminating
beam can also be modulated to put an image on the retina. Thus it becomes
possible to perform microperimetry, relating the areas where a stimulus
is seen or not seen directly to the retinal image and to the presence
of retinal scarring.27 Optical Coherence Tomography (OCT) A different form of optical imaging is involved in Optical Coherence Tomography (OCT). This
technique does not produce a fundus image but uses
a low-coherence light beam to provide cross-sectional information in
a way that is analogous to ultrasound B-scan. Because the wavelength
of light is so much smaller than ultrasound wavelengths, it can produce
far higher resolution and can be used to identify the relationship between
layers of the retina and choroid.28 |