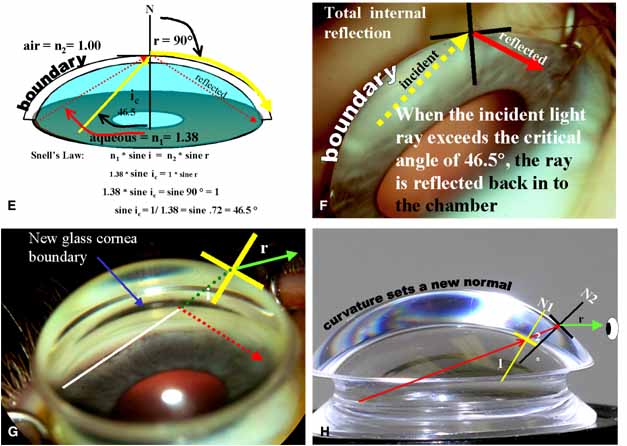
Fig. 2b Continued. E. As the incident ray increases, at some point the refracted ray is bent 90 degrees and does not emerge, the critical angle, (yellow arrow). Solving for sine i reveals the critical angle is 46.5 degrees. Any incident ray of light that exceeds the critical angle (red arrow) will be reflected back into the eye. Beyond the critical angle, the cornea acts as a mirror and reflects, not refracts the light. N = normal. F. Light rays emanating from the chamber angle always exceed the critical angle and are reflected back into the eye; this is total internal reflection of light rays. This concept applies to light reflected down a fiber optic cable. G. The index of refraction of a Koeppe lens is approximately 1.4, almost exactly that of the cornea. According to Snell's law, the incident ray travels through the goniolens practically unaltered (dotted green line) because the index of refraction of the cornea and Koeppe are almost the same. The ray escapes because the angle of incidence at the new Koeppe air boundary is now less than the critical angle. When a new normal is constructed at the interface of the contact lens and air (yellow intersecting lines), the critical angle is no longer exceeded because the dome of the Koeppe is steeper than the cornea. Koeppe = 50 diopters. H. This is easier to visualize by simply studying the shape of the Koeppe lens. The curvature of the surface dome is greater than that of the cornea. The steeper dome of the Koeppe creates a new normal (N2) whose angle of incidence (2) is less than the critical angle and angle 1, thus the ray emerges (green arrow) into the air. (N1) normal where critical angle is exceeded. (Figure continues.)