1. Stenstrom S: Investigation of the variation and the correlation of the optical elements
of human eyes. Am J Optom Arch Am Acad Optom 25:218, 1948 2. Sorsby A, Benjamin B, Davey JB, et al: Emmetropia and Its Aberrations. London, Her Majesty's Stationery Office, 1957 3. Sorsby A, Benjamin B, Sheridan M: Refraction and Its Components During the Growth of the Eye From the Age
of Three. London, Her Majesty's Stationery Office, 1961 4. Sorsby A, Leary GA: A Longitudinal Study of Refraction and Its Components During Growth. London, Her Majesty's Stationery Office, 1970 5. Mutti DO, Zadnik K, Adams AJ: Myopia. The nature versus nurture debate goes on. Invest Ophthalmol Vis Sci 37:952, 1996 6. Steiger A: Die Entstehung der sphärischen Refraktionen des menschlichen Auges. Berlin, Karger, 1913 7. Sorsby A, Sheridan M, Leary GA: Vision, visual acuity and ocular refraction of young men. Br Med J 1:1394, 1960 8. Zadnik K, Mutti DO, Friedman NE, Adams AJ: Initial cross-sectional results from the Orinda Longitudinal Study
of Myopia. Optom Vis Sci 70:750, 1993 9. Zadnik K, Manny RE, Yu JA, et al for the CLEERE Study Group: Ocular component data in schoolchildren as
a function of age and gender. Optom Vis Sci 80:226, 2003 10. Fledelius HC: Pre-term delivery and the growth of the eye. An oculometric study of eye size around term-time. Acta Ophthalmol 204(Suppl):10, 1992 11. Gernet H: Achsenlänge und refraktion lebender augen von neugeborenen. Albrecht von Graefes Arch Ophthalmol 166:530, 1964 12. Larsen JS: The sagittal growth of the eye. I. Ultrasound measurement of the depth
of the anterior chamber from birth to puberty. Acta Ophthalmol 49:239, 1971 13. Larsen JS: The sagittal growth of the eye. II. Ultrasonic measurement of the axial
diameter of the lens and the anterior segment from birth to puberty. Acta Ophthalmol 49:427, 1971 14. Larsen JS: The sagittal growth of the eye. IV. Ultrasonic measurement of the axial
length of the eye from birth to puberty. Acta Ophthalmol 49:873, 1971
15. Luyçkx J: Mesure des composantes optiques de l'oeil du nouveau-né
par échographie ultrasonique. Arch Ophthalmol (Paris) 26:159, 1966
16. Blomdahl S: Ultrasonic measurements of the eye of the newborn infant. Arch Ophthalmol 57:1048, 1979 17. Inagaki Y: The raid change of corneal curvature in the neonatal period and infancy. Arch Ophthalmol 104:1026, 1986 18. Insler MS, Cooper HD, May SE, Donzis PB: Analysis of corneal thickness and corneal curvature in infants. CLAO J 13:182, 1987 19. Mandell RB: Corneal contour of the human infant. Arch Ophthalmol 77:345, 1967 20. York MA, Mandell RB: A new calibration system for photokeratoscopy. Part II—corneal curvature
measurements. Am J Optom Arch Am Acad Optom 46:818, 1969 21. Zadnik K, Mutti DO, Fusaro RE, Adams AJ: Longitudinal evidence of crystalline lens thinning in children. Invest Ophthalmol Vis Sci 36:1581, 1995 22. Norton TT: Experimental Myopia in Tree Shrews, pp 178–199. Chichester, UK, John Wiley and Sons, 1990 23. Troilo D, Nickla DL, Wildsoet CF: Form deprivation myopia in mature common marmosets (Callithrix jacchus). Invest Ophthalmol Vis Sci 41:2043, 2000 24. Smith EL, Hung L-F: The role of optical defocus in regulating refractive development in infant
monkeys. Vision Res 39:1415, 1999 25. Wallman J, Adams JI: Developmental aspects of experimental myopia in chicks: susceptibility, recovery
and relation to emmetropization. Vision Res 27:1139, 1987 26. Rabin J, Van Sluyters RC, Malach R: Emmetropization: a vision-dependent phenomenon?Invest Ophthalmol Vis Sci 20:561, 1981 27. Schaeffel F, Glasser A, Howland HC: Accommodation, refractive error, and eye growth in chickens. Vision Res 28:639, 1988 28. Gwiazda J, Thorn F, Bauer J, Held R: Emmetropization and the progression of manifest refraction in children
followed from infancy to puberty. Clin Vis Sci 1993; 8:337–344. 29. Plomin R, DeFries JC, McClearn GE: Behavioral Genetics, pp 256–259, 315–325. New York, WH Freeman and Company, 1990 30. Mutti DO, Mitchell GL, Moeschberger ML, et al: Parental myopia, near work, school achievement, and children's refractive
error. Invest Ophthalmol Vis Sci 43:3633, 2002 31. Zadnik K, Satariano WA, Mutti DO, et al: The effect of parental history of myopia on children's eye size. JAMA 271:1323, 1994 32. Saw SM, Wu HM, Seet B, et al: Academic achievement, close up work parameters, and myopia in Singapore
military conscripts. Br J Ophthalmol 85:855, 2001 33. Saw SM, Zhang M, Hong R, et al: Near-work activity, night-lights, and myopia in the Singapore-China
study. Arch Ophthalmol 120:620, 2002 34. Angle J, Wissmann DA: Age, reading, and myopia. Am J Optom Physiol Opt 55:302, 1978 35. Angle J, Wissmann DA: The epidemiology of myopia. Am J Epidemiol 111:220, 1980 36. Richler A, Bear JC: Refraction, nearwork and education. A population study in Newfoundland. Acta Ophthalmol 58:468, 1980 37. Zadnik K, Mutti DO, Adams AJ, et al: Parental history and myopia: taking the long view [letter to the editor—in
reply]. JAMA. 272:1256, 1994 38. Schwartz M, Haim M, Skarsholm D: X-linked myopia: Bornholm eye disease. Linkage to DNA markers on the distal part of Xq. Clin Genet 38:281, 1990 39. Sertie AL, Quimby M, Moreira ES, et al: A gene which causes severe ocular alternations and occipital encephalocele (Knobloch
syndrome) is mapped to 21q22.3. Hum Mol Genet 5:843, 1996 40. Sertie AL, Soss V, Camargo AA, et al: Collagen XVIII, containing an endogenous inhibitor of angiogenesis and
tumor growth, plays a critical role in the maintenance of retinal structure
and in neural tube closure (Knobloch syndrome). Hum Mol Genet 9:2051, 2000 41. Young TL, Ronan SM, Drahozal LA, et al: Evidence that a locus for familial high myopia maps to chromosome 18p. Am J Hum Genet 63:109, 1998 42. Young TL, Ronan SM, Alvear AB, et al: A second locus for familial high myopia maps to chromosome 12q. Am J Hum Genet 63:1419, 1998 43. Naiglin L, Gazagne C, Dallongeville F, et al: A genome wide scan for familial high myopia suggests a novel locus on chromosome 7q36. J Med Genet 39:118, 2002 44. Mutti DO, Semina E, Marazita M, et al: Genetic loci for pathological myopia are not associated with juvenile myopia. Am J Hum Genet 112:355, 2002 | 

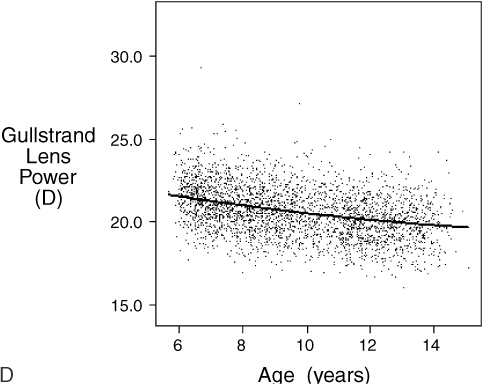
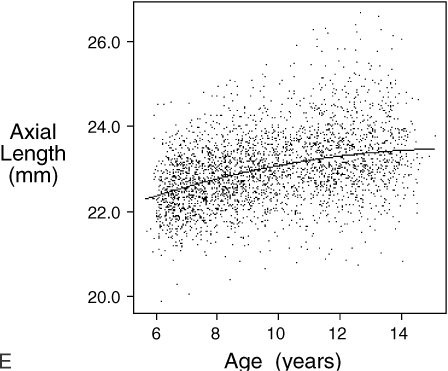
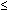 .01) than children with only one or no myopic parent.
.01) than children with only one or no myopic parent.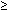 50 Diopter Hours (D-hrs) of Near Work Compared With < 50 D-hrs
Per Week.
50 Diopter Hours (D-hrs) of Near Work Compared With < 50 D-hrs
Per Week.